Вот мысль появилась. Для начала задачку немного упростить стоит.
Есть матрица
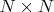
, задан параметр
![$l \in [1, N-1]$ $l \in [1, N-1]$](https://dxdy-02.korotkov.co.uk/f/1/9/1/191650e98e1c8b822f26b18e56e2acdb82.png)
заполнена следующим образом:
![$\forall~i: a_{ij} = 1,~j \in [i, i+l]$ $\forall~i: a_{ij} = 1,~j \in [i, i+l]$](https://dxdy-04.korotkov.co.uk/f/f/c/f/fcfda91545ea21f53a4d8d3455fdb91182.png)
.

соответствуют

. Остальные элементы

.
Т.е. первая строчка:

единица,

нулей. Каждая следующая строчка получена путем циклического сдвига вправо предыдущей.
Считаем число ненулевых столбцов 0, при выборе

строк.
1) Выбрав
![$n, n \in [1, N]$ $n, n \in [1, N]$](https://dxdy-04.korotkov.co.uk/f/7/4/a/74a1784ca145093bbef63bbb1e350cf982.png)
строк, можно получить
![$k, k \in [min\{N, l+1\}, min\{N, n(l+1)\}]$ $k, k \in [min\{N, l+1\}, min\{N, n(l+1)\}]$](https://dxdy-04.korotkov.co.uk/f/7/2/a/72a61f364786eeb659677423210216fc82.png)
ненулевых столбцов.
2') Зафиксируем
![$n, n \in [1, N]$ $n, n \in [1, N]$](https://dxdy-04.korotkov.co.uk/f/7/4/a/74a1784ca145093bbef63bbb1e350cf982.png)
. Выбрав именно

строк, получить

ненулевых столбцов, идущих подряд, можно количеством способов:

,
где

- количество

-значных чисел (допускаются числа с нулями в начале) в

-ичной системе счисления, у которых сумма цифр равна

Это в терминологии, использованной в книге Н. Я. Виленкина. Существует у этого числа несколько свойств и рекуррентная формула, с помощью которых число несложно посчитать.
Но два вопроса остаются в силе:
2) Фиксируем
![$n, n \in [1, N]$ $n, n \in [1, N]$](https://dxdy-04.korotkov.co.uk/f/7/4/a/74a1784ca145093bbef63bbb1e350cf982.png)
. Сколько существует способов выбрать именно

строк, чтобы получить

ненулевых столбцов (не обязательно, чтобы столбцы шли подряд)?
3) Сколько существует способов выбора строк, чтобы получить

ненулевых столбцов (не обязательно, чтобы столбцы шли подряд)?
4) Есть идеи?
