Единственность поля комплексных чисел

[qwerty1917]

Здравствуйте, есть следующее доказательство единственности поля комплексных чисел. Не могу уловить сути, почему операции производятся не над векторами. После первого слова "очевидно" становится непонятно, откуда это все получилось. Эквивалентна ли данная теорема теореме " все расширения поля действительных чисел ℝ, полученные присоединением к полю решения уравнения $x^2+1\ =\ 0$ к ℝ изоморфны между собой.
Каждое ассоциативное коммутативное кольцо К с единицей 1 без делителей нуля, являющееся двумерным векторным пространством над ℝ изоморфно полю ℂ.

Доказательство. Без ограничения общности отождествим $1\ast\mathbb{R}\ с $\mathbb{R}$ и считаем $\mathbb{R}\ вложенным в К.
Так как ${dim}_\mathbb{R}К = 2$, то существует е ϵ К\$\mathbb{R}$ такой, что 1 и е составляют базис пространства К над $\mathbb{R}$.
Очевидно, $e^2=\ \alpha\ast1+2\beta\aste$ с $\alpha,\ \beta\ \epsilon\ \mathbb{R}$. Для элемента $ f\ =\ e\ -\ \beta\ \notin\ \mathbb{R}$ имеем $f^2=\lambda$, где $\lambda\ =\ \alpha+{\ \beta}^2\epsilon\ \mathbb{R}\ . Очевидно, $\lambda<0,$ поскольку иначе $\sqrt{\lambda\ }\ \ \epsilon\ \mathbb{R}$ и мы имели бы $f=\ \pm\sqrt\lambda$. Таким образом существует $σ \notin\ \mathbb{R}$, для которого $\sigma^2=-\lambda^{-1}$. Теперь $j^2\ =\ -1$ для $j=\ \sigma f$, и легко проверяется ( как при построении ℂ), что каждый ненулевой элемент из К обратим, т.е. К – поле.
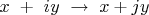
Отображение $\mathbb{C}\ \rightarrow\ K$, определенное соответствием $x\ +\ iy\ \rightarrow\ x+jy$, является изоморфизмом полей.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы) - обозначения нужно набирать тоже как формулы (и не кириллицей), бэкслэш в TeXе - это не способ экранирования символов, а первый символ команды, не надо вставлять его перед пробелами и т.п.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.