Здравствуйте,
в Ландау Лифшице выводится формула для потенциальной энергии через период, с помощью решения интегрального уравнения. Все там нормально и вроде понятно до того момента, когда "интеграл по dE вычисляется элементарно и оказывается равным

".
Подскажите пожалуйста, какие математические правила позволяют поменять пределы интегрирования в таком равенстве:
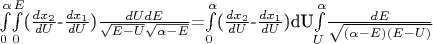
То есть были пределы от 0 до E, а стали от U до

. Каким образом?