Ряска
1. Пусть энергия взаимодействия отдельной частицы с остальными зависит только от концентрации частиц:

2. Концентрация частиц в центрально симметричном случае зависит только от расстояния до центра:

3. Сила действующая на частицу со стороны других частиц:

Вода.
1. (тут какие-то рассуждения про теорему Гаусса в двумерном случае).
2.

, где A - характеристика струи
3. Сила действующая на ряску пропорциональна квадрату скорости

, далее
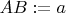
Условие равновесия частицы.

(1)
Посмотрим на форму

.
1. С ростом концентрации, энергия должна расти.
2. Но при некоторой концентрации

дальнейшему сближению мешают "хвостики" листьев и энергия частицы устремляется в бесконечность.
3. Подходящая функция

Подставляем в (1)

тогда


- константа интегрирования, которая зависит от начальных условий.... на границе прудика и от начальной концентрации ряски.
На радиусе
![$r = \sqrt[3]{\frac{3a}{C}}$ $r = \sqrt[3]{\frac{3a}{C}}$](https://dxdy-01.korotkov.co.uk/f/8/5/5/85569f535d10227a71669e4026f5304582.png)
концентрация становится нулевой, а значит будет нулевой и на меньших радиусах - отрицательной концентрации не бывает.
Можно "поиграться" с другими видами
