syaomyao, ну раз уж вам интересно.
Идея: давайте возьмём две прямые, исходящие из вершин

и

, которые пересекаются в

внутри треугольника. Допустим, что возможна ситуация, как на рисунке. Ну подъедем тогда точкой

в отрезок
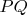
. Рисунок развалится моментально. Значит, такого не бывает.
Формально:Пусть заданы два луча

и

, исходящие из

и

и идущие внутрь треугольника. Их точка пересечения

. Рассмотрим множество пар точек

,

таких, что

и

,

. Для каждой такой пары можно построить точку

следующим образом: через

проводим прямую вдоль

, через

проводим прямую

,

.
1) Покажите, что геометрическое место точек

для всех допустимых пар

представляет собой отрезок с началом в

. Обозначим его второй конец

.
2) Что можно сказать о расстоянии

?