Пусть

- заданная последовательность замкнутых попарно непересекающихся непустых подмножеств отрезка
![$[0,1]$ $[0,1]$](https://dxdy-03.korotkov.co.uk/f/a/c/f/acf5ce819219b95070be2dbeb8a671e982.png)
(

- натуральный ряд).
Лемма. Если отрезок
![$[a,b]\subseteq[0,1]$ $[a,b]\subseteq[0,1]$](https://dxdy-01.korotkov.co.uk/f/0/b/2/0b275b9d7ff2c272a5f2ccccfbc1df7d82.png)
таков, что
![$[a,b]\cap F_k\neq\varnothing$ $[a,b]\cap F_k\neq\varnothing$](https://dxdy-01.korotkov.co.uk/f/c/2/a/c2a65bda116ec8d0cffdd892367d7b2e82.png)
, а

для некоторого

, то отрезок
![$[a,b]$ $[a,b]$](https://dxdy-04.korotkov.co.uk/f/f/e/4/fe477a2781d275b4481790690fccd15f82.png)
не покрывается никаким конечным подсемейством
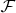
.
Доказательство следует из того, что такое покрытие, очевидно, содержит больше одного элемента, и связности отрезка.

Предположим, что для некоторого

уже построен отрезок
![$I_{n-1}=[a_{n-1},b_{n-1}]$ $I_{n-1}=[a_{n-1},b_{n-1}]$](https://dxdy-02.korotkov.co.uk/f/1/b/8/1b8803077a9f23aae30ccfd1e784da4982.png)
, не покрываемый никаким конечным подсемейством
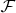
и удовлетворяющий условию

(для
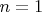
у нас имеется отрезок
![$I_0=[0,1]$ $I_0=[0,1]$](https://dxdy-01.korotkov.co.uk/f/4/8/e/48e327b7c644862957a31f8cc21ead7882.png)
). Построим отрезок
![$I_n=[a_n,b_n]$ $I_n=[a_n,b_n]$](https://dxdy-03.korotkov.co.uk/f/6/4/c/64ce122cdac8365e733e3b3744a29eb382.png)
следующим образом.
Если

, то полагаем

(выполнение перечисленных условий в этом случае очевидно).
Пусть

. По предположению,

не покрывается семейством

, поэтому найдётся точка

. Более того, можно считать, что
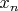
не совпадает ни с

, ни с

, так как разность

является непустым открытым подмножеством

и, следовательно, содержит некоторый интервал. Далее определяем
![$$a_n=\begin{cases}\frac{a_{n-1}+x_n}2\text{, если }F_n\cap[a_{n-1},x_n]=\varnothing\text{,}\\ \max(F_n\cap[a_{n-1},x_n])\text{, если }F_n\cap[a_{n-1},x_n]\neq\varnothing\text{,}\end{cases}$$ $$a_n=\begin{cases}\frac{a_{n-1}+x_n}2\text{, если }F_n\cap[a_{n-1},x_n]=\varnothing\text{,}\\ \max(F_n\cap[a_{n-1},x_n])\text{, если }F_n\cap[a_{n-1},x_n]\neq\varnothing\text{,}\end{cases}$$](https://dxdy-01.korotkov.co.uk/f/0/3/f/03f2492f52c5ab0b7cb888131080211882.png)
![$$b_n=\begin{cases}\frac{x_n+b_{n-1}}2\text{, если }F_n\cap[x_n,b_{n-1}]=\varnothing\text{,}\\ \min(F_n\cap[x_n,b_{n-1}])\text{, если }F_n\cap[x_n,b_{n-1}]\neq\varnothing\text{.}\end{cases}$$ $$b_n=\begin{cases}\frac{x_n+b_{n-1}}2\text{, если }F_n\cap[x_n,b_{n-1}]=\varnothing\text{,}\\ \min(F_n\cap[x_n,b_{n-1}])\text{, если }F_n\cap[x_n,b_{n-1}]\neq\varnothing\text{.}\end{cases}$$](https://dxdy-04.korotkov.co.uk/f/3/b/d/3bded03418c985a2b17adf25687f1f5082.png)
Заметим, что хотя бы одно из множеств
![$F_n\cap[a_{n-1},x_n]$ $F_n\cap[a_{n-1},x_n]$](https://dxdy-04.korotkov.co.uk/f/7/c/8/7c8dfe6b24ffd270691c3ba3aa7abd3f82.png)
или
![$F_n\cap[x_n,b_{n-1}]$ $F_n\cap[x_n,b_{n-1}]$](https://dxdy-01.korotkov.co.uk/f/c/d/a/cdae2d6b09cdaf5c17ed7e7275a40ee182.png)
не пусто, поэтому либо

, либо

. Поэтому отрезок
![$I_n=[a_n,b_n]$ $I_n=[a_n,b_n]$](https://dxdy-03.korotkov.co.uk/f/6/4/c/64ce122cdac8365e733e3b3744a29eb382.png)
удовлетворяет условиям леммы и, следовательно, не покрывается никаким конечным подсемейством
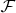
. Кроме того,

. Поэтому мы можем продолжать построение дальше.
Дополнительно заметим, что в случае

выполняются условия

,

и, следовательно,

. Так как такие

образуют бесконечную подпоследовательность натурального ряда
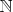
, из этих условий следует, что

(в силу компактности отрезка), и что

, то есть, семейство
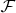
не покрывает отрезок

.