Моделирование движения в поле 2 тел

[eugrita]

Моделируется плоское движение точечной массы в силовом поле 2 масс (планет). (или если угодно движение отрицательного заряда в поле 2 положительных зарядов)
Начальное положение точки на линии центров вдоль оси х планет
$\vect{r_0}=[x_0,0]$
начальная скорость перпендикулярна линии центров. $\vec{v_0}=[0,v_{0y}]$
Уравнения движения в безразмерных единицах имеют вид
$ \ddot{x}=-(1-m) \cdot \frac{x}{r_1^3} -m \cdot \frac{x-1}{r_2^3} $
$\ddot{y}=-(1-m) \cdot \frac{y}{r_1^3} -m \cdot \frac{y}{r_2^3} $
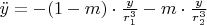
$ r_1=\sqrt{x^2+y^2 }$ и $ r_2=\sqrt{(x-1)^2+y^2}$
где $ m=\frac{M_1}{M_2}$ отношение масс (или зарядов)
В случае силового поля 1 массы как известно траектории -эллипсы или гиперболы.
При данной форме начальных условий их оси параллельны оси х
Критерием вида траектории является величина эксцентриситета орбиты
для нашей формы начальных условий проще вычислить параметр
$ k=0.5 \cdot x_0 \cdot v_{0y}^2 $
если $ k<1 $ движение финитное по эллипсу
если $ k>1 $ -инфинитное по гиперболе.
Так в основном и было при моделировании силового поля 2 масс (Земля-Луна)
Но при некоторых сочетаниях параметров $ k, x_0 $
получаются необъяснимые эффекты.
1) орбита хотя и замыкается но не гладко, т.е. по направлению скорости отличаются
2)при моментах старта близком к Луне $ x_0=0.85, k=1.05 $ и
$ x_0=0.95, k=1.21 $ движение все равно финитное несмотря, что
$ k>1 $ и у траекторий похожих на эллипсы наибольшая ось повернута по отношению к оси х.
Мне кажется, при расположении точки старта и центов масс на 1 прямой и начальной скорости ей перпендикулярной это невозможно хотя бы из соображений симметрии.
На погрешность и шаг численных методов не могу списывать. Случаи проверялись, шаг интегрирования уменьшался до тысячных. Все оставалось.
В чем дело? Можно ли написать формулу на основе выражения потенциальной и кинетической энергии выражающую критерий финитного и инфинитного движения?

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- исправьте вставку картинки.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.