Если Вы о рентгеноструктурном анализе кристаллов, то там используется лишь электронная плотность

и её фурье-образ, см.
https://ru.qwe.wiki/wiki/X-ray_crystall ... ion_theory .
Да, я в частности о РСА.
Никакие межэлектронные корреляторы там не фигурируют.
Простите, а как Вы электронную плотность посчитаете?! В минимальном случае (с плохонькой точностью) нужны плотности из модели Томаса-Ферми на каждом атоме, а для приличного согласия нужно тяжеловесными квантово-химическими расчётами их делать. Именно электронная структура атомов и молекул -- это электронная корреляция в явном виде.
Об электронах каких энергий Вы говорите? Рассеяние на ядре, какое оно? Если чисто кулоновское, то это не интересно.
Обычно используемых (порядка 10 кэВ). Да, на ядре оно кулоновское, скучное, о чём я Вам и сообщил. В первом Борновском же приближении просто добавляется рассеяние на электронной плотности (собственно, поэтому зная рентгеновские сечения рассеяния на атомах, можно в грубом приближении получить и электронные).
Пожалуйста, дайте ссылки на описание экспериментальных технологий измерения межэлектронных корреляций в многоэлектронном атоме или молекуле. Нужно больше конкретики.
Для начала Вы бы конкретно пояснили за то, что называете "межэлектронными корреляциями", т.к. Ваша терминология, по ходу дела, очень отличается от общепринятой.
Но, допустим, возьмём пример, который я уже привёл:
типа Оже-распада,
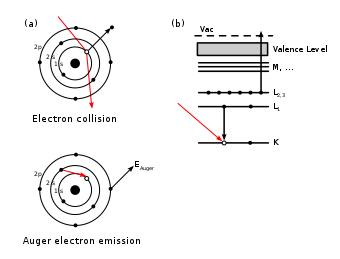
Рентгеном выбивается электрон с, например, 1s (K) уровня какого-то атома (можно в молекуле). Получается уровень с дыркой, очень высоковозбуждённое электронное состояние. Далее один электрон сваливается в эту дырку, но за счёт электронной корреляции, лишняя энергия уносится каким-то связанным электроном.
А что лазер? Вы пропускаете луч через кювету с веществом, засекаете падение интенсивности и судите о спектрах поглощения. В каком состоянии был атом до поглощения фотона, чистом или смешанном, в каком он оказался после? Это всё Вы домысливаете исходя из парадигмы. Нужны целевые эксперименты, направленные на проверку самой парадигмы. Где они?
Спектры поглощения -- это самое простое и банальное из того, что люди делают. Давайте Вы поясните какую именно парадигму Вы хотите проверить, а то получается разговор ни о чём. Но самые фундаментальные эксперименты на тему проверки основ квантовой механики обычно делаются на фотонах, и к сожалению я не специалист в подобных вещах. Атомно-молекулярные эксперименты же обычно нацелены именно на изучение атомов и молекул, но если Вы поясните что Вам надо из этой области, я вероятно смогу отослать Вас к нужным экспериментальным техникам.