На конечном упорядоченном множестве

отличных элементов осуществляется
одна перестановка, переводящая первичный порядок во вторичный, в результате которой
каждый элемент меняет позицию. Вопрос заключается в числе вариантов

осуществления этой
единственной перестановки, меняющей первичный порядок множества на вторичный.
Есть такой ответ:
![$V_n=[\frac{n!}{e}+\frac{1}{2}]$ $V_n=[\frac{n!}{e}+\frac{1}{2}]$](https://dxdy-04.korotkov.co.uk/f/7/b/d/7bddf24333fadccbf5708a1c029f45ce82.png)
, тут [ ] – целая часть числа, или, иначе говоря:

переходит в

при точном целом приближении.
Есть другой ответ:

.
Хотелось бы доказать.
* Работает для:
n = 1; Множество {1}. Изменить положение элементов нельзя.
![$V_1=[\frac{1!}{e}+\frac{1}{2}]=0$ $V_1=[\frac{1!}{e}+\frac{1}{2}]=0$](https://dxdy-03.korotkov.co.uk/f/a/a/1/aa173546da9b3bcc1be0eb34ba70fcfc82.png)
,

;
n = 2; Множество {12}. Изменить положение элементов можно лишь одним способом: {21}.
![$V_2=[\frac{2!}{e}+\frac{1}{2}]=1$ $V_2=[\frac{2!}{e}+\frac{1}{2}]=1$](https://dxdy-04.korotkov.co.uk/f/7/a/7/7a72731470462e193db51a43e5d17dfb82.png)
,

;
n = 3; Множество {123}. Изменить положение можно двумя способоми: {231} и {312}.
![$V_3=[\frac{3!}{e}+\frac{1}{2}]=2$ $V_3=[\frac{3!}{e}+\frac{1}{2}]=2$](https://dxdy-02.korotkov.co.uk/f/5/7/2/57211c8d20432bb6d02524d85646ab6682.png)
,

;
n = 4; Множество {1234}. Изменить положение можно 9 способоми: {2143}, {2341}, {2413}, {3142}, {3412}, {3421}, {4123}, {4312} и {4321}.
![$V_4=[\frac{4!}{e}+\frac{1}{2}]=9$ $V_4=[\frac{4!}{e}+\frac{1}{2}]=9$](https://dxdy-01.korotkov.co.uk/f/c/5/6/c56620add024e7f458082de74e410dda82.png)
,

;
n = 5; Множество {12345}. Изменить положение можно 44 способоми: перебрать на листке минут за 5–10 не составит труда.
![$V_5=[\frac{5!}{e}+\frac{1}{2}]=44$ $V_5=[\frac{5!}{e}+\frac{1}{2}]=44$](https://dxdy-03.korotkov.co.uk/f/e/8/d/e8d85a7a00f24a2db1a37f51bb214e3582.png)
,

;
** Для: n = 0; Множество {} пустое. Вопрос открытый, поскольку значения

"кажутся" разными:
![$V_0=[\frac{0!}{e}+\frac{1}{2}]=0$ $V_0=[\frac{0!}{e}+\frac{1}{2}]=0$](https://dxdy-02.korotkov.co.uk/f/1/d/7/1d703bb16b62b3570ebf642ac03c6ac882.png)
,

;
Переставлять при n = 0 вроде бы нечего, но и при одной воображаемой перестановке "ничего" в "ничём" ни у кого из ничего не возникнет проблем пересечений со своим первичным положением.
*** Кроме того, любопытно, что

можно представить как

где

:

;

;

;

;

;
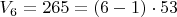
;

;

;

;

и т.д.