Из
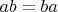
следует, что группа абелева и что любой её элемент представляется в виде

. Из остальных двух соотношений вытекает, что можно считать

и

. Таким образом, порядок группы уже

.
Далее, для любого

справедливо

. Значит, порядок группы есть степень двойки и, следовательно,

.
Получается, что возможностей для

не так уж и много.
1)

,

;
2)

,

;
3)

;
4)

;
5)

.
В этом перечислении только 3 циклических группы:

,

и

. Наверное, надо просто посмотреть, что ни одна из них не подходит (или, наоборот, какая-то подходит).