Обоснование сходимости,нахождение предела последовательности

[klazius_]

Помогите , пожалуйста , не знаю как действовать в подобные задачи.
Понимаю, что нужно доказать сходимость и монотонность , но как к этому подступиться не знаю .
Можете дать какое- нибудь направление для действий или источник,где разбираются подобные примеры .
Задание: обосновать сходимость и найти придел последовательности
1.$ A_1=1 , A_{n+1} = 2/(4+A_n)$
2.$A_1=1.1 ; A_{n+1}= \sqrt{3\code A_n - 2}$

[thething]

Во-первых, формулы набирайте правильно, ничего же непонятно.

Во-вторых, в таких задачах полезно сперва "поверить", что предел есть и перейти к пределу в рекуррентном соотношении. Придёте к квадратным уравнениям, решение которых даст то, на что можно ориентироваться.

В частности, в первом пункте покажите по индукции, что $A_n$ чем-то ограничено сверху (снизу), а, доказав, что $A_{n+1}-A_n$ сохраняет знак, полУчите монотонность.

Во втором пункте покажите по индукции, что $1\leq A_n\leq2$, и доказывайте монотонное возрастание, рассматривая ту же разность (это если я правильно интерпретировал написанное).

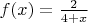
Дополнение по первому пункту (коль скоро стало ясно, о чём идёт речь). По-видимому, тут последовательность скачет туда-сюда и монотонности нет, поэтому докажите, что $0\leq A_n\leq1$ а потом примените принцип сжимающих отображений к функции $f(x)=\frac{2}{4+x}$.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задач.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.