Цитата:
Последующее развитие дифференциального и интегрального исчисления представляет собой загадочное исключение из нормального процесса упрощения в математике. Сейчас мы имеем намного менее элегантную систему, которая принижает использование бесконечных рядов и усложняет систему правил для дифференцирования и интегрирования. Правила для дифференцирования всё ещё полны, при наличии разумного набор операций для построения функций, но правила для интегрирования неполны до убожества. Их недостаточно, чтобы проинтегрировать такие простые алгебраические функции, как
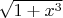
, или даже рациональные функции с неопределёнными постоянными, как
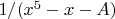
. Более того, только в последние десятилетия мы смогли понять, какие алгебраические функции можно проинтегрировать по нашим правилам. (Этот малоизвестный результат изложен Дэвенпортом (1981).)
Цитата:
The subsequent development of calculus is a puzzling exception to the normal process of simplification in mathematics. Nowadays we have a much less elegant system, which downplays the use of infinite series and complicates the system of rules for differentiation and integration. The rules for differentiation are still complete, given a sensible set of operations for constructing functions, but the rules for integration are pathetically incomplete. They do not suffice to integrate simple algebraic functions like
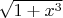
, or even rational functions with undetermined constants like
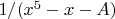
. Moreover, it is only in recent decades that we have been able to tell which algebraic functions are integrable by our rules. (This little-known result is expounded by Davenport (1981).)
Stillwell, John.
Mathematics and Its History. 3rd. ed. New York: Springer, 2010. Print. Undergraduate Texts in Mathematics.
Прав ли Стиллвелл (Стиллуэлл)? Действительно ли анализ деградировал? Не следует ли нам вернуться к Ньютону и Лейбинцу?
