Задача про момент инерции

[Daylikor]

Помогите, пожалуйста, решить задачу
На тонком стержне длиной а укреплен шар радиусом r так, что расстояние между его центром и осью вращения, перпендикулярной длине стержня, равно а. Определить относительную погрешность в определении момента инерции, если шар считать точечной массой. Длина стержня а = 10 r, масса шара в 10 раз больше массы стержня.

Мой ход решения:
Пусть, $m$-масса шара, тогда масса стержня равна $0,1m$
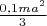
Момент инерции стержня относительно его конца равен $\frac{0,1ma^2}{3}$, а момент инерции шара, относительно его центра масс соответственно равен $\frac{2mr^2}{5}$. Также я нашел момент инерции шара, во втором случае считаемого материальной точкой, относительно оси вращения, расположенной на другом конце стержня $ma^2$
По теореме Гюйгенса-Штейнера можно определить момент инерции шара относительно оси вращения, расположенной на другом конце стержня. Он будет соответственно равен сумме момента инерции шара относительно его центра масс( $\frac{2mr^2}{5}$ ) и произведения массы этого шара на расстояние между осями( $ma^2$ )
Я так понимаю, что для определения относительной погрешности нужно из момента инерции, при котором шар не является материальной точкой, вычесть момент инерции, при котором шар является материальной точкой.
Теперь вопрос: Как это сделать? Это должен быть момент инерции системы тел шар+стержень, или просто момент инерции шара относительно оси вращения, расположенной на другом конце стержня? Если это просто момент инерции шара, то тогда зачем нам дана масса стержня, а если это именно момент инерции системы тел, то тогда как его определить?

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы/обозначения (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.