Вопрос про один предел

[eprivalo]

Рассмотрим предел:
$\lim\limits_{n \to \infty}^{}\frac{n^\frac{n}{k}}{n!}$
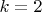
При $k = 1 $ это плюс бесконечность. При $k = 2$ он равен нулю. Возникли такие вопросы:
- существует ли k при котором этот предел конечен и отличен от нуля?
- если "да", то какое это k и чему равен предел?

У меня ощущение, что это должно быть что-то стандартное и давно изученное, но решить не смог.

[Lia]

eprivalo в сообщении #1415988 писал(а):

При $k = 1 $ это плюс бесконечность. При $k = 2$ он равен нулю.

Попытки решения хотелось бы видеть хотя бы для этих $k$.

[ewert]

eprivalo в сообщении #1415988 писал(а):

У меня ощущение, что это должно быть что-то стандартное и давно изученное

Вполне возможно. Но почему бы тупо не взять логарифм от этой дроби?...

Знаменатель породит сумму логарифмов, т.е. приблизительно интеграл от логарифма, т.е. примерно $n\ln n$.

По-моему, после этого вопрос насчёт $k$ автоматически снимается.

[eprivalo]

Lia в сообщении #1415993 писал(а):

eprivalo в сообщении #1415988 писал(а):

При $k = 1 $ это плюс бесконечность. При $k = 2$ он равен нулю.

Попытки решения хотелось бы видеть хотя бы для этих $k$.

При k=1 очевидно.
При k=2 переписываем в виде $\frac{(2n)^n}{(2n)!}$, доказываем, что $\frac{2n}{(k+1)(2n-k)}\leqslant1$, при этом $\frac{2n}{n(n+1)}\to0$

-- 19.09.2019, 17:42 --

ewert в сообщении #1415998 писал(а):

eprivalo в сообщении #1415988 писал(а):

У меня ощущение, что это должно быть что-то стандартное и давно изученное

Вполне возможно. Но почему бы тупо не взять логарифм от этой дроби?...

Знаменатель породит сумму логарифмов, т.е. приблизительно интеграл от логарифма, т.е. примерно $n\ln n$.

По-моему, после этого вопрос насчёт $k$ автоматически снимается.

Спасибо, попробую