Будем рассматривать (задачу неоднородного линейного приближения)
Поделим все на

. Обозначим

,
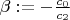
. Рассмотрим

Если хочется решать задачу для любых

и

, то существенно потребовать иррациональности

(т. е. несоизмеримости
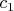
и

). В случае

цепные дроби для поиска решений мало помогут. Не знаю можно ли в общем случае предложить что-то кроме перебора (см. ниже). Конечно достаточно дробной частью

приблизить дробную часть

и тогда

определяется однозначно. Это приводит к задаче на окружности: сделать величину

малой в смысле метрики

на окружности

.
Например, можно действовать как при доказательстве плотности иррационального поворота окружности: разбить окружность (длины 1) на

полудуг длины

; тогда по принципу Дирихле точка

при целых
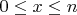
хотя бы дважды попадет в одну из этих полудуг (пусть это происходит при
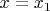
и

). А дальше уже можно идти с шагом

(строго меньше

), пока не придем в полудугу, содержащую

. Будем считать, что
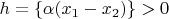
и
![$\beta \in [0,1]$ $\beta \in [0,1]$](https://dxdy-03.korotkov.co.uk/f/e/8/c/e8c0e23225d6788dea6b9420b47f033282.png)
. Осталось найти

так, что

. Ответ:

. Формально мы справились за

итераций (на деле же все упирается в точность вычислений). Это лучше тупого перебора

от 0 до упора и вот почему.
Можно показать, что если

диофантово с показателем
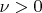
, т. е. для некоторого

и всех целых

и натуральных

выполнено
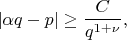
то у неоднородной задачи существует решение

(на самом деле решение будет существовать в любом интервале длины

). Для случая
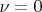
это есть у Хинчина в "Цепные дроби" (теорема 26). Множество диофантовых с показателем
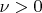
чисел имеет полную меру Лебега. Для не диофантовых (=лиувиллевых чисел, составляющих множество меры нуль) актуальная граница может быть выше любой степени

.