Цитата:
Определение 3.3. Для аффинного пространства

и двух непустых подмножеств

и

пространства

будем говорить, что гиперплоскость
 разделяет (соответственно, строго разделяет)
разделяет (соответственно, строго разделяет)  и
и 
, если

лежит в одном, а

— в другом из двух полупространств (соответственно, открытых полупространств), определяемых

.

На рисунке 3.3 (а) два замкнутых выпуклых множества

и

неограниченны и оба асимптотические к гиперплоскости

. Гиперплоскость

есть разделяющая гиперплоскость для

и

, но

и

невозможно строго разделить. На рисунке 3.3 (б)

и

выпуклы и замкнуты,

неограниченно и асимпотическое к гиперплоскости

, а

ограниченно. Гиперплоскость

строго разделяет

и

. Гиперплоскость

тоже разделяет

и

, но нестрого.
Не понимаю, почему на (а)

не разделяет строго и на (б)

не разделяет строго. Пусть наше афинное пространство двухмерное,

задано как

,

задано как
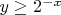
. Для любого

имеем

, то есть

не пересекает

. Чего я не понимаю?
Цитата:
Для гиперплоскости

и любой непостоянной аффинной формы

, задающей

(то есть

), можно определить два подмножества

и

называемые
(замкнутыми) полупространствами, определяемыми 
.
Цитата:
Если дана гиперплоскость

и любая непостоянная аффинная форма

, задающая

(то есть

), вспомните, что мы определяем
замкнутые полупространства, определяемые 
, как

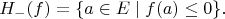
Мы также определяем
открытые полупространства, определяемые 
, как два множества

