Heat kernel for an infinitesimal interval(не ясны переходы)

[trikotash]

Книга Geometry_topology_and_Physics_Mikio_Nakahara_2nd_Edition_2003, тема интегралы по траекториям бозонов(с.41) не ясны переходы после разложенной в ряд экспоненты:

Если Вам очевиден этот переход-просьба: объяснить. Я понимаю, что нужно оставить ряд до второго члена(считая с нуля),но как уходят, например, операторы дифференцирования мне совершенно не ясно.
Заранее спасибо!

[Gickle]

Чтобы легче было видеть, что происходит, вынесите $-i\varepsilon$ в первом выражении под интегралом, а потом вспомните формулу Тейлора:

$$f(x) = f(a) + f'(a)(x-a) + \ldots$$

Ну и потом вспомните разложение экспоненты.

[trikotash]

Gickle в сообщении #1409484 писал(а):

Чтобы легче было видеть, что происходит, вынесите $-i\varepsilon$ в первом выражении под интегралом, а потом вспомните формулу Тейлора:

$$f(x) = f(a) + f'(a)(x-a) + \ldots$$

Ну и потом вспомните разложение экспоненты.

Большое Вам спасибо за то, что обратили внимание на мой вопрос. К сожалению я,по неосторожности, выложил не все картинки - за что прошу прощения!



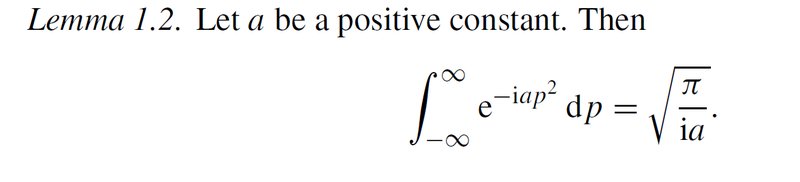
Так будет верно!
Мне не ясен переход от разложенной в ряд экспоненты, так как мы раскладываем до n=2, у нас остаются члены с операторами дифференцирования в разных степенях и степень эпсилон при них вторая или ниже, куда они уходят? Например член :$~ (d/dx)^4$

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.