А, понятно! Звёздочка там, где в индексной нотации стоит "сворачивающий индекс".
Вроде не обязательно.
Я не очень понимаю, чем вышеуказанное объяснение плохо. Не всегда, но часто звёздочка обозначает индуцированное отображение: отображению (морфизму) пространств

соответствует отображение структур над этими пространствами, которое обозначается
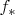
или
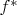
в зависимости от того, в ту же сторону действует индуцированное отображение или в обратную.
Единственная неточность -- то, что этих обозначений всего два, а структур много. Обычно какая именно структура -- или ясно из контекста, или написано явно (например,

), или может быть при необходимости обозначено ещё каким-нибудь символом.
Рекомендую книжку Новиков, Тайманов, "Современные геометрические структуры и поля", это более современная версия "современной геометрии".