Помогите понять, где я ошибаюсь.
Вы ошибаетесь там, где называете

углом.
Но аналогия с тригонометрическими функциями есть.
1) Тригонометрические функции.
Рассмотрим окружность

. Пусть

— точка пересечения окружности с осью

,

— произвольная точка окружности. Обозначим

удвоенную площадь сектора

, взятую со знаком "

", если

отсчитывается в положительном направлении, и со знаком "

" — если в отрицательном. Тогда

— это абсцисса, а
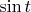
ордината точки

.
2) Гиперболические функции.
Рассмотрим одну ветвь гиперболы

,

. Пусть

— точка пересечения этой ветви с осью

,

— произвольная точка этой ветви. Обозначим

удвоенную площадь гиперболического сектора

, взятую со знаком "

", если точка

находится в полуплоскости
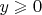
, и со знаком "

" — если в полуплоскости

. Тогда

— это абсцисса, а

— ордината точки

.