О кубической функции

известно, что среди касательных к её графику существует только единственная касательная, угловой коэффициент которой равен

, причём абсцисса точки касания
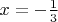
. Кроме этого известно, что данная кубическая функция имеет экстремум в точке

. Определите коэффициенты

,

и

.

. Угловой коэффициент равен производной функции.



Так как по условию это точка касания, то

.


. Так как абсцисса точки касания
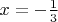
, то, подставив в выражение производной, имеем:


. Если в точке

имеется экстремум, то

(вот в этом я не уверен).

Получил систему из 3-ёх уравнений:



Решив её получил

,

,

. Но проверка не проходит
