Четырьмя короткими числами, возможно, большое число.

[Tpxp]

$ 1) $ Двоичное число $ 010010=18 $ (в десятичной системе счисления).
$ 2) $ Если преобразовать в такой вид (каждая единичка отдельно с тем же колличеством нулей) - $ 010000 000010 $.
$ 3) $ Если перемножить то получиться в числе одна единичка, проще получить складывая номер разряда $ 2+5=7 $ т.е. получится число $ 1000000 $.
$ 4) $ Если число $ 010010 $ преобразовать в прогрессию по колличеству разрядов в группе чисел - $ (000000) (00000) (0000) (000) (00) $. Перечисление номера разрядов начинается с $ … 8, 7 , 6 , 5 , 4 , 3 , 2, 1 $ .
- нумерация разрядов начинается с право на лево. Т.е. первый разряд преобразуется в два разряда, третий разряд преобразуется в три разряда, четвёртый разряд преобразуется в четыре разряда и тд.
$ 6) $ То для $ 1) $ получится число $ (0000000) (111111) (00000) (0000) (111) (00) $. Перечисление номера разряда с право на лево $ … (6; 5; 4) (3; 2) $ и тд.
Это число преобразуется, как по $ 2) $
$ (0000000) (100000) (00000) (0000) (000) (00) $

$ (0000000) (010000) (00000) (0000) (000) (00) $

$ (0000000) (001000) (00000) (0000) (000) (00) $

$ (0000000) (000100) (00000) (0000) (000) (00) $

$ (0000000) (000010) (00000) (0000) (000) (00) $

$ (0000000) (000001) (00000) (0000) (000) (00) $

$ (0000000) (000000) (00000) (0000) (100) (00) $

$ (0000000) (000000) (00000) (0000) (010) (00) $

$ (0000000) (000000) (00000) (0000) (001) (00) $
Перемножая эти числа получится одна единичка, вместо перемножения можно сложить их номер разрядов.


$ 4 $ числами записывается -
у $ 1) $ колличество единиц в строке и $ 3) $ получившиеся единички номер разряда.
У $ 6) $ колличество единиц и номер разряда у получившейся единички по $ 7 $)


Может ли при произвольном колличестве разрядов при различных комбинациях существовать более одной комбинации, по предположению одна комбинация образуется.


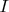
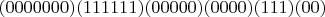
В данном случае первый номер $ I $ группы разрядов - $ (0000000) (111111) (00000) (0000) (111) (00) $. (группа $ (111111) $ $ 5 $ группа из $ 6 $ единичек, равна $ 16 $.
$\left\lbrace \frac{I^{2}+I}{2}+1 \right\rbrace$ - ( $ I +1 $ равно количеству единичек в группе ).


Чтобы найти суммы к примеру
$ (0000000) (111111) (00000) (0000) (111) (00) $
$ ... (21;20;19;18;17;16) (15;14;13;12;11) (10;9;8;7) (6;5;4) (3;2) $
$ (…; 5; 4; 3; 2; 1) $ - перечисление группы единичек которые в скобках. (Для указания количества единичек в одной $ I $ группе требуется прибавить $ 1 $ )


$ \frac{(10+7)}{2}*4=34 $ т.е. суммы $ 10+9+8+7=34 $. ($ 10 $ и $ 7 $ числа слево и справо в группе и нахождение среднего деля на два, $ 4 $ это колличество единиц в группе).
$ \frac{ (21+16)}{2}*6=111 $ (т.е. $ 6 $ единичкаим принадлежит в группе $ 16+17+18+19+20+21=111 $ ) т.е. уравнение-
$\left\lbrace \frac{I^{3}+3*I^{2}+4*I+2}{2}=S_{I} \right\rbrace $ - сумма вторичной последовательности т.е. сумма $ 2+3=5, 4+5+6=15 $, $ 7+8+9+10=34 $.


$ 256 $ разрядов данных архивируются до $ 128 $ и параллельно архивируются $ 256 $ разрядов до $ 128 $ разрядов. В сумме будет $ 128+128=256 $ эти полученные данные в сумме архивируются до $ 128 $ разрядов. К полученным $ 128 $ разрядам прибавляются $ 128 $ разрядов архивированных данных ранее $ 256 $ разрядов т.е. в сумме получается $ 128+128=256 $ и их архивирвать до $ 128 $ разрядов и так бесконечно, возможно добавлять данные безмерно.
Типа , что-то чёрной дыры возможно. Но данные которые древние сложно извлечь потребуется бесконечное время при бесконечном колличестве таких архивирований последовательных. Возможно метки добавить через каждые гигобайт данных и тд. (При методе сортировке). Не то чтобы $ 256 $ разрядов преобразуются в $ 128 $, они вроде бы в меньшее количество могут преобразоваться колличеству разрядов, возможно сокращаются до $ 64 $ разрядов. (Вроде бы только два числа в основном требуется). (Но алгоритм не проверин на работоспособность) (Т.к. только сортировка, но и внём для одной сортировки требуется большое количество времени, возможно). (По структуре предполагаю, что, вроде бы, возможно.).


Если алгоритм нормально работает. -количество единичек + их сумма по номеру разрядов. При $ 64 $ разрядах примерно начинается эффективность при меньших разрядах, вроде бы не умещается количество единичек + их сумма по номеру разрядов либо несколько раз возможно архивировать прежде произвести новое сложение дополнительных данных.


Квантовые компьютеры вроде бы могут такие числа раскладывать по различным разрядам одновременно?
(Т.е. уравнение два найдены , до не мог создать программу без этих двух уравнений. Теперь , возможно более менее проверить на 20 разрядах не так много. Но может не достаточно, т.к. учитывая тип простых чисел и существание для него уравнения довльно таки непростые, мало-ли может иначе при больших чисел комбинации иначе.).

([img][IMG]https://s8.hostingkartinok.com/uploads/images/2019/04/7afeb1a3f9e34e093191cbdaedc96924.png[/img][/img]

https://pikabu.ru/story/kogda_ponimaesh_chto_yeto_vesit_64_kilobayta_4194242







Новую систему последовательности обнаружил, возможно.

$ 2 $ $ 3 $ $ 5 $ $ 8 $ $ 16 $ $ 29 $ $ 53 $ $ 98 $ $ 180$ $ 331 $ - все предыдущие числа их сумма образуют чуть меньшее число. (три предыдущих числа складываются, в данном случае).

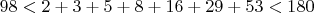
$ 98<2+3+5+8+16+29+53<180 $ - т.е. образуется интервал. Все предыдущие суммы скапливаются в интервале 98 - 180. Т.е. известно максимальное число.
Вычитая его, можно дальше найти максимальное число.
Складываются три числа предыдущих, чтобы образовать данное число.




Если два числа скласть чуть меньше получится. Т.е. $ 2<3+5<=8 $ Т.е. чуть смещено.
Т.е. данная система последовательности в данном отношении не идеально применяется. Но , что-то такое ищу систему последовательностей. Слишком большие суммы типа все суммы предыдущих чисел слишком большие суммы образуют для следующего числа, по сравнению с $ 2^{n} $ , $ n= $ от $ 0 $ до бесконечности .



Можно было дробные числа суммировать, для меньшего образования числа по всем предыдущим числам, необходимо существование уравнения образования числа. Тогда число всех сумм было бы меньше двойки в степени и имело прогрессию по разрядам. И все предыдущие суммы скапливались в одном интервале с известным максимальным числом. Вычитая данное максимальное число можно дальше вычитать известные максимумы.

Предполагаю образовать две суммы $ 3 $ и $ 4 $ (предыдущие суммы) для исключения некоторых комбинаций непростых.
Так же применять последовательность через два, каждое первое число как отметка и применяется постоянно.


Первое указанное вид подсчёта распределено в большом интервале. Так уж не знаю как решить. Но предположил одну сортировок. Это вычитать наибольшее число и так далее, если при вычитании числа образуется отрицательное число, то надо вычитать следующее более меньшее число, если снова отрицательное, то снова чуть меньшее надо вычитать. В конечном итоге , возможно образуется одно число, если оно не соответствует данному набору то надо снова вычитать взяв чуть меньшее число и вычитать так же последовательно.















Применил два раза функцию $\left\lbrace \frac{I^{3}+3*I^{2}+4*I+2}{2}=S_{I} \right\rbrace $ от полученного порядковых чисел от $ 1 $ до $ n $ у номера разрядов в двоичном числе образуются числа при $ 2 $ или $ 3 $ единичках непересекающиеся данные, т.е. надо записывать $ 6 $ чисел , наверно. Т.е. $ f=S_{I} $ , $ F=f(S_{I}) $.
Т.е. если даже систему при максимальном количестве разрядов $ 512 $ складывать единички $ 2 $ или $ 3 $ в различной комбинации, то у них не образуются пересекаемости, но не возможно найти комбинацию так просто, возможно.
Вот программа - https://my-files.ru/wekx0q В данной программе складываются три единички из формул при 20 максимальных разрядах. мало, но больше не позволяет программа Delphi 7. (программа не доработана). Т.к. при трёх суммах или двух чисел при максимальных разрядах $ 714 $ комбинаций всего-лишь.
Первая таблица-
Перечисление строк, второе перечисление количества единичек в групповом числе, третие начало числа в группе чисел, четвёртое сумма груп чисел т.е. в некотором интервале, пятое применение уравнения второй раз и получение начало числа у определёной группы, шестое применение по второму уравнению и получение числа и получение суммы группы числа т.е. в интервале, но уже при втором применение уравнения $\left\lbrace \frac{I^{3}+3*I^{2}+4*I+2}{2}=S_{I} \right\rbrace $.
Вторая таблица это нумерация строчек, второе количество единичек при различных комбинациях, трертие это уравнение первый раз применённое $\left\lbrace \frac{I^{3}+3*I^{2}+4*I+2}{2}=S_{I} \right\rbrace $ с складыванием в различных комбинациях трёх единичек, четвёртое это уравнение второй раз применённое $\left\lbrace \frac{I^{3}+3*I^{2}+4*I+2}{2}=S_{I} \right\rbrace $ с складыванием в различных комбинациях трёх единичек.
Эти полученные числа образуют пересекаемость или не пересекаемость, может известно.
Т.к. у данного преобразованного числа $ (0000000) (111111) (00000) (0000) (111) (00) $ по сравнению с обычным $ 010010 $ больше или столько же комбинаций. Не могу понять данный случай. У данного числа $ (0000000) (111111) (00000) (0000) (111) (00) $ значительно больше комбинаций , вроде бы. Т.к. оно возможно больше и больше параметров и в нём больше комбинаций и т.к. больше по количеству разрядов, может.

Label справо показыает количество пересекаемостей при сумме трёх единичек т.е. ноль.


Если при комбинациях при максимальном количестве разрядов $ 1 000 000 $ всё нормально , то если каждый из разрдов перечислять номером из $ 1000 $ разрядов, если единички, а если ноль то все тысяча разрядов равны нулю. То образуется $ 1 000 000 000 $ разрядов этого достаточно, чтобы определить, вроде бы максимумы чисел. Либо что-то не так, так как при миллионе разрядов невозможно на компьютере подсчитать количество комбинаций в различных случаях. (При двадцати в лучшем случае $ 3 $ сумм кобинаций единичек возможно подсчитать на Delphi $ 7 $ .).
При этом образуемое число может уместится , где-то в $ 4000 $ разрядах значительно меньше от начального.
И с помощью алгоритма f1(100%)+f2(100%)->50%+50%->f3(100%)->50%+f4(100%)->50%+50%->100%->f5(100%)->50%...…… безмерно вмещать информацию. На данный момент сложно, может , что-то не учтено.
Не могу понять, если число структурированно и потом больше по количеству разрядов (потенциально т.к. в одной группе образуется большее количество единичек, но они все единички) у него больше количеств комбинаций или нет. И образуется записывание количества единичек в числе, но оно уже динамическое и постоянно меняется у преобразованного числа и всегда отличается по сравнению с двоичным числом , записав у него количество единичек.)

Дело в том , что прогрессия у преобразованного числа $ (0000000) (111111) (00000) (0000) (111) (00) $ знаительно меньше и при некотором максимальном разряде к примеру при триллионе разрядов, можно число возвести в ту же степень , что и колличество разрядов максимальное и при этом оно может оказаться их суммы меньше, возможно.








Возможно применить такую модель числа. 10 групп чисел по 1000 разрядов и в каждой группе одна единичка. Эти 10 групп с 10 единичками задают один из параметров.
Далее для каждой из строк древа распределения. Т.е. применяется по минимуму количество единичек, но в большем количестве разрядов в числе, что возможно облегчит поиск распределения единичек т.к. их по минимуму. (Т.е. в интервале 1000 разрядов в группе одна единичка).
Далее у данной архивации числа, можно записать полученные ~240 номеров разрядов и получится не более 10 килобайтов данных, а может и килобайт.

[Lia]

Оформите задачу здесь, без сторонних ссылок и вставки картинок.
Заодно и сформулируете.
Попытки решения также необходимы.

[Lia]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.