RIP писал(а):
...тогда уж как классы эквивалентности фундаментальных последовательностей рациональных чисел.
Да, конечно же классы.
Кстати, с сечениями тоже получается классы. Но можно и без классов.
Я извиняюсь за возможные повторы, но совершенно нет сил перечитывать весь тред с начала (с самого первого сообщения темы). Так что заранее извиняюсь, если что-то повторю.
Нам на первом курсе давали так:
Сечением называется пара  , такая что
, такая что  ,
,  и
и 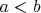 для любых
для любых  и
и  .
.
Если принять это определение, то каждый рациональный элемент

задаётся двумя различными сечениями, ибо сам определяемый элемент может лежать как в левой, так и в правой компоненте пары. После этого приходится объявлять действительными числами множество классов эквивалентности

Однако надо заметить, что в сечении

множество

однозначно восстанавливается по

, так что упоминать

в определении --- лишнее. Я бы предпочёл оформить всё это дело так:
Непустое множество  с непустым дополнением
с непустым дополнением  называется действительным числом, если для любых
называется действительным числом, если для любых  и
и  из
из  следует
следует  и
и 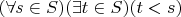 .
.
Раньше я предпочитал брать в качестве действительного числа начальный сегмент вместо конечного, но кто-то мне сказал, что с конечными сегментами проще определять операции. Дескать, со знаками меньше возни.
А вот что воистину гадко --- это определять элементы

как бесконечные десятичные дроби. После такого определения легче повеситься, чем вводить на

операции.