Зорич V 3.14 a)

[Paul Ivanov]

Определяем рекурсивно конечные разности $g_k(x)$ порядка $k$ функции $f$ следующим образом:

$$g_1(x)=f(x+h_1)-f(x)$$

$$g_2(x)=g_1(x+h_2)-g_1(x)$$

$$. . .$$

$$g_k(x)=g_{k-1}(x+h_k)-g_{k-1}(x)$$

(где $h_1,h_2,...,h_k\in\mathbb{R}$)
Отсюда имеем для первых двух разностей в точке $x_0$ следующие формулы:

$$g_1(x_0)=f(x_0+h_1)-f(x_0)$$

$$g_2(x_0)=g_1(x_0+h_2)-g_1(x_0)=(f(x_0+h_1+h_2)-f(x_0+h_2))-(f(x_0+h_1)-f(x_0))$$

И да, я не ошибся (также, как и учебник), если выстраивать конечные разности так, как мне предлагали здесь (с чем я когда-то поспешил согласиться): post1343356.html , то тогда легко придумать контрпример, опровергающий то, что требуется доказать в пункте а) далее.

а) Известно, что все возможные аргументы функции $f$ (а именно $x_0, x_0+h_1, ...$), используемые при определении $g_n(x_0)$, лежат на отрезке $[a,b]\subset\mathbb{R}$ и длина этого отрезка минимально возможная, а также, что $f\in C^{(n-1)}[a,b]$ и существует $f^{(n)}(x)$ хотя бы при любом $x\in(a,b)$.
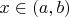
Нужно доказать, что тогда найдётся точка $\xi\in[a,b]$ такая, что $g_n(x_0)=f^{(n)}(\xi)h_1h_2...h_n$
Есть две идеи, которые потенциально могут помочь, но которые я не знаю, как развить:
1. Если доказываемое утверждение неверно, то согласно теореме Дарбу для любого $x\in[a,b]$ $g_n(x_0)>f^{(n)}(x)h_1h_2...h_n$ (или для любого $x\in[a,b]$ $g_n(x_0)<f^{(n)}(x)h_1h_2...h_n$
2. Можно $f(x)$ разложить в ряд тейлора с остаточным членом в форме лагранжа, и представить в такой форме каждое слагаемое, на которые раскладывается $g_n(x_0)$, тогда большая часть сократится и останутся только n-ные производные, но что с этим делать всё равно непонятно.
Вообще здесь видимо нужно построить некую дополнительную функцию от $x$, n-ная производная которой оборачивается в нуль в некоторой точке отрезка $[a,b]$, одним из слагаемых которой является сама функция $f(x)$. Подобный трюк используется при доказательстве интерполяционной формулы Эрмита, которую можно найти по следующей ссылке в разделе "Ошибка" : https://ru.wikipedia.org/wiki/%D0%AD%D1 ... 0%B8%D1%8F

[Paul Ivanov]

Ларчик просто открывался. Решение найдено здесь: https://mathoverflow.net/questions/3313 ... 365#331365