мера иррациональности µ(π) = 2 ?

[Руст]

С наскоку доказать, что $\mu(\pi)=2$, мне кажется малоприподъемным.
Я так не думаю. Доказательство относится к более широкой теории, называемой мною теорией равномерности.
Я 15 лет назад в общих чертах разработал такую теорию для доказательства ГР.
Для достаточно общей дважды гладкой функции $f(x)$ разбиваем площадь под кривой сеткой на квадраты со стороной $\frac{1}{n}$,
и считаем площадь в единицах площади квадрата и количество целых точек. Доказывая, что их разница оценивается $O(\sqrt{n} \log(n))$
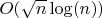
получаем много приложений. Когда функция обратима имеет рациональное суммирование типа $\tg(x+y)=\frac{\tg(x)+\tg(y)}{1-\tg(x)\tg(y)}$, $(\tg(x))'=1+\tg^2(x)$
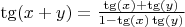
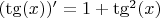
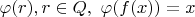
получаются оценки на рациональные приближения обратной функции $\varphi(r), r\in Q, \ \varphi(f(x))=x$. В этом смысле получим меру иррациональности не только для $\pi$,
а для значений широко класса (обратной) функции в рациональных точках.
В принципе я могу изложить части неопубликованной теории заходя 2-3 раза в неделю на час.

Сегодня изложу самую элементарную часть о ряде Фаррея. В принципе почти все это можно найти в некоторых книгах по теории чисел.
Под рядом Фаррея $\Phi_n$ подразумевают множество положительных рациональных чисел $\frac{a}{b}, a\le n, b\le n$.
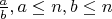
Считаем, что все рациональные числа представляются несократимой дробью, с положительным знаменателем.
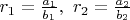
Два рациональных числа $r_1=\frac{a_1}{b_1}, \ r_2=\frac{a_2}{b_2}$ называем соседними, если не существует рациональных чисел $r=\frac{a}{b}$
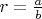
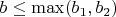
в интервале $(r_1,r_2)$ со знаменателем $b\le \max(b_1,b_2)$. Рациональное число с минимальным знаменателем между $r_1$ и $r_2$ есть $r=\frac{a_1+a_2}{b_1+b_2}$.
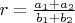
Легко показать, что соседние рациональные числа являются соседними рациональными числами. Каждое рациональное число из ряда Фаррея является средним от своих
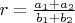
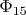
соседей слева и справа $r=\frac{a_1+a_2}{b_1+b_2}$. Отметим, что среднее может быть сократимым. Пример в ряде Фаррея $\Phi_{15}$ число $\frac{5}{9}$ находится между $\frac{8}{15}$ и $\frac{2}{3}$.

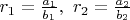
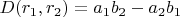
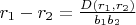
Для двух рациональных чисел $r_1=\frac{a_1}{b_1}, \ r_2=\frac{a_2}{b_2}$ введем понятие дискриминанта как определитель матрицы из элементов числителя (первая строка) и знаменателя (вторая строка), т.е. $D(r_1,r_2)=a_1b_2-a_2b_1$. Разница выражается через дискриминант $r_1-r_2=\frac{D(r_1,r_2)}{b_1b_2}$. Знак дискриминанта показывает ориентацию расположения
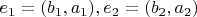
двух векторов $e_1=(b_1,a_1), e_2=(b_2,a_2)$, дискриминант соответствует площади параллелограмма и равна количеству целых точек в параллелограмме, когда внутренние точки считаются с весом 1, точки на ребрах с весом $\frac{1}{2}$, вершины параллелограмма с весом $\frac{1}{4}$. Внутренние точки определяют так же количество рациональных точек (точнее лучей) между ними со знаменателем не превосходящим максимума их знаменателей.
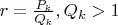
Вообще, для любого рационального числа $r$, разлагая в цепную дробь получим $r=\frac{P_k}{Q_k}, Q_k>1$. Это число имеет только два соседа со знаменателем меньше $Q_k$, а именно
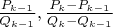
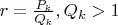
$\frac{P_{k-1}}{Q_{k-1}}, \frac{P_k-P_{k-1}}{Q_k-Q_{k-1}}$. Само число $r=\frac{P_k}{Q_k}, Q_k>1$ является соседом с меньшим знаменателем для чисел $\frac{mP_k+P_{k-1}}{mQ_k+Q_{k-1}}, m\in Z, m\neq 0, -1$.

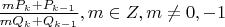
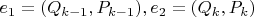
Вообще для любого разложения в цепную дробь базис векторов $e_1=(Q_{k-1},P_{k-1}), e_2=(Q_k,P_k)$ площадь и количество целых точек в параллелограмме равны 1 и они могут быть использованы в подсчете целых точек вместо базиса $(1,0), (0,1)$.
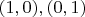
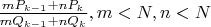
Ряд Фаррея между этими базисами по сути эквивалентны $\frac{mP_{k-1}+nP_k}{mQ_{k-1}+nQ_k}, m<N,n<N$ и $\frac{m}{n}, m<N,n<N$.
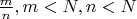
На сегодня все.

[SomePupil]

(Оффтоп)

Руст, такие вещи надо писать в виде статей, нет?..

[Руст]

Руст, такие вещи надо писать в виде статей, нет?..

Я публиковал эти и некоторые последующие вещи в электронном журнале. Не помню только где и внес ли в истину.

Я когда написал об эквивалентности рядов Фаррея, не указал в каком смысле. Пусть имеются две пары рациональных чисел $r_1=\frac{a_1}{b_1}, r_2=\frac{a_2}{b_2}$ (фиксированные)
и $\frac{m_1}{n_1}, \frac{m_2}{n_2},$ все $m_1,n_1,m_2,n_2$ положительные и ограничены.
Тогда все дроби $\frac{a_1m_1+a_2n_1}{b_1m_1+b_2n_2}, \frac{a_1m_2+a_2n_2}{b_1m_2+a_2n_2}$ находятся в интервале $(r_1,r_2)$, причем порядки и расстояния соответствует порядкам и расстояниям через пропорциональность дискриминантов

$$Dis(\frac{a_1m_1+a_2n_1}{b_1m_1+b_2n_2}, \frac{a_1m_2+a_2n_2}{b_1m_2+a_2n_2})=Dis(\frac{a_1}{b_1}, \frac{a_2}{b_2})Dis(\frac{m_1}{n_1},\frac{m_2}{n_2}).$$

Это взгляд на рациональные числа как элементам проективного пространства над $Z$, т.е. $Q= P^1Z= Z^2/Z$. Сопоставляя рациональному числу вектор наклона ("скорость")
многое становится более наглядным, в частности разные суммы.

[Руст]

По сути это соответствует тому, что определитель произведения матриц
$\begin{pmatrix} a_1 & a_2\\ b_1 & b_2\\ \end{pmatrix}$ и
$\begin{pmatrix} m_1 & m_2\\ n_1 & n_2\\ \end{pmatrix}$
является произведением определителей. В то же время определяет количество целых точек в параллелограмме, когда целые точки на вершинах параллелограмма
учитываются с весом $\frac{1}{4}$, на ребрах $\frac{1}{2}$, только внутренние с весом 1.
Если $\frac{a_1}{b_1}, \frac{a_2}{b_2}$ соседние то нет ни внутренних, ни на ребрах, все 4 вершины входят с весом $\frac{1}{4}$.
В любом многоугольнике с вершинами в целых точках разница между площадью и количеством целых точек равна нулю.
Направление диагонали $\frac{a_1+a_2}{b_1+b_2}$
соответствует диагонали параллелограмма (называется медиантой) и для соседних рациональных чисел оно соответствует
рациональному числу с минимальным знаменателем между ними.

Теперь можно начать новую тему $g-$ суммы. Функция $g(x)$ определяется как $g(x)=0, x\in Z, \ g(x)=\{x\}-\frac{1}{2}, \ x\not \in Z$.
Похожая функция есть в книге Карацуба "Аналитическая теория чисел" $\rho(x)=-g(x), x\not \in Z$.
Целые точки х соответствуют точкам разрыва, и функция $g(x)$ нормализована в целых точках как средняя от левого и правого предела (в отличии от $\rho(x)$). И это свойство
важно для некоторых приложений. Название $g-$ функции возникло как буква после $e$, где $e(x)=e^{2\pi x}$.
Соответственно, под $g-$ суммой понимается $\sum_{x\in Z} g(f(x))$. В отличии от $e-$ суммы, $g-$ суммы инвариантны относительно модулярных преобразований:
$z=a_1y-b_1x, \ t=a_2y-b_2x$, где $\frac{a_1}{b_1}, \frac{a_2}{b_2}$ соседние рациональные число.