мера иррациональности µ(π) = 2 ?

[maxal]

В препринте Irrationality Measure of Pi предлагают доказательство, что мера иррациональности $\mu(\pi)=2$.

Основной результат я не проверял, но вот доказательство леммы 4.1 (якобы усиливающей мою теорему 2) у меня вызывает вопросы. Это дает основания подозревать, что и в основном результате что-то нечисто.

[g______d]

Я не понял самой последней фразы в доказательстве леммы: как он от подпоследовательности $q_k$ переходит ко всем $n$.

[grizzly]

Там если кликнуть на авторе, можно найти куда более впечатляющие результаты в других его работах. Или вот здесь ещё он "общается" с сообществом MO -- никого не напоминает? :)

[maxal]

grizzly, спасибо! Теперь всё встало на свои места

[RIP]

На самом деле действительно достаточно рассматривать только $n=p_k$, что следует из теоремы Лежандра: Если $\left\lvert\alpha-\frac{p}{q}\right\rvert<\frac{1}{2q^2}$, то $p/q$ — подходящая дробь к $\alpha$. Другое дело, что при $\mu(\pi)=1+u/v$ ничего хорошего не получится.

[maxal]

Еще один препринт с места в карьер обсуждающий, что $\mu(\pi)<2$, т.е. ставящий под сомнение трансцендентность $\pi$. Фундаментаментальная работа на 50+ страниц.

[maravan]

maxal
А ваша статья уже проверена?

Можно дать по ней замечания?

[maxal]

maravan
Кем проверена? А замечания всегда приветствуются.

[maravan]

maxal
Например, рецензентами или математическим сообществом.

Теорема 2 сформулирована так, будто утверждения выполняются для всех достаточно больших $ n $.
Но в статье доказательство даёт оценку только для большинства $ n $, а на бесконечном множестве хороших приближений $ \pi $ поведение другое.

На мой взгляд, Теорема 2 по сути верна, но её формулировка в статье слишком сильная: она скрывает подпоследовательности, на которых оценки не работают.
В корректной форме я бы явно указывал, что результат справедлив для всех больших $ n $, кроме бесконечного, но редкого множества, связанного с приближениями $ \pi $.

Можно, например взять такой ряд:

$$ \sum _{n=1}^{\infty } \frac{1}{n^3 | \sin (n)| ^{2.4}}. $$

Если он сходится, то верна оценка:

$$ \mu(\pi)\leqslant1+\frac{3}{2.4}=2.25. $$

Или я не прав?

[maxal]

maravan
Можно сказать, что "проверена" - научное сообщество работу цитирует, ошибок никто не нашел.
Насчет формулировки, я не вижу в ней ничего "некорректного". Вероятно, вы имеете в виду какое-то другое (более общее?) утверждение, но его существование не делает мою теорему некорректной.
Если вы считаете, что результат можно усилить, то лучше написать свою статью. Однако, я бы рекомендовал для начала ознакомится со статьями цитирующими мою, так как с 2011 года было несколько (попыток) обобщений (включая очевидную лажу, к сожалению).

[Руст]

Просмотрел как новую работу, где якобы доказывается $\mu(\pi)=2$ так и работу maxal.
Первая полная чушь.
В работе maxal нет грубых ошибок, но полно мелких замечаний.
1. В определении меры $\mu(x)$ как
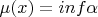
$\mu(x)=inf \alpha$, число рациональных $\frac{p}{q}$ (или пар целых $p,q>0$), таких что выполняется соотношение
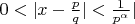
$0<|x-\frac{p}{q}|<\frac{1}{p^{\alpha}}|$ конечно. Тут не требуется положительность $x$, не требуется взаимная простота чисел $p,q$.
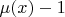
Я бы мерой иррациональности числа х назвал число $\mu(x)-1$. Тогда мера иррациональности рациональных чисел равнялось бы нулю как и положено, а для иррациональных х
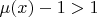
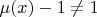
их мера иррациональности больше или равно 1. Кстати числа х, имеющие меру иррациональности $\mu(x)-1>1$ или $\mu(x)-1 \neq 1$ составляют меру 0.
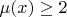
2. Часто говорится о транцендентности числа, если $\mu(x)\ge 2$. Транцендентность не причем, для всех иррациональных.
3. Используются в обозначении действительных чисел (меры иррациональности) $m,k$. Обычно они используются для целых чисел.
Результат сходимости или расходимости рядов такого вида известен многим. Кажется я об этом (о связи сходимости таких рядов с мерой иррациональности числа $\mu(\pi)$)
говорил и на форуме и самому maxal лет десять, может больше назад.

[RIP]

Кстати, теорему 5 maxalа можно уточнить. Если $v\geqslant1$, то неравенство $\mu(\pi)<1+\frac{u}{v}$ влечёт не только стремление $\frac{1}{n^u\lvert\sin(n)\rvert^v}$ к нулю, но и сходимость ряда. Это следует из работы Харди и Литтлвуда https://link.springer.com/article/10.1007/BF02940594 (леммы 3 и 4). Более общая ситуация рассматривается в статье Крузе https://eudml.org/doc/204799.

[maxal]

Руст в сообщении #1703249 писал(а):

В работе maxal нет грубых ошибок, но полно мелких замечаний.

Рецензентов не было, вот и результат :)

[Руст]

Дело в том, что в работе maxal нет ошибок, но и нет ничего не известного ранее.
Если сходится или расходится (это не доказано и доказательство сходимости или расходимости ни чем не легче), то $\mu(\pi)=$.

Я могу предложить путь для доказательства $\mu(\pi)=2$.
1. Функции тангенс и котангенс имеют простую формулу суммирования.
2. Если $tang(x)=u$ или котангенс , то легко выражается через u $tang(nx)=u$, а так же производная функции.
Следовательно, методом Ньютона находится квадратичное приближение. Даже не будучи дробью правильного разложения в непрерывную дробь, позволяет оценить коэффициенты $q_n$ через значения правильной дроби $\frac{P_n}{Q_n}\approx \pi$. Отсюда скорее всего получим $\mu(\pi)=2$ или хорошую верхнюю оценку для него.
Мне некогда этим заниматься. Надеюсь сам maxal или Rip могут реализовать эту идею.

[maxal]

Руст
Да, я не сказал ничего нового по существу, но, видимо, приведенные аргументы по поводу сходимости этого ряда раньше не были явно прописаны, раз люди активно цитируют мой препринт. По другому я это не могу объяснить.

Насчет меры иррациональности $\pi$ - это отдельный большой вопрос со множеством публикаций. Такие гранды как Doron Zeilberger и Wadim Zudilin в 2020 году доказали лишь, что $\mu(\pi) \leq 7.104$, что является наилучшей оценкой на данный момент. С наскоку доказать, что $\mu(\pi)=2$, мне кажется малоприподъемным, если вообще возможным, так как совсем не факт, что мера равна именно 2м.