критерий выбора знака при решении уравнений 4 степени

[kotenok gav]

Знаю.

[dmd]

Поправьте меня если не прав, но по-моему уравнение 4-й степени тригонометрически не решабельно. Есть и другие формулы четверного угла, под которые замену подобрать тоже нереально. И на math.stackexchange.com ничего кроме этого не находится.

[verywell]

dmd в сообщении #1378499 писал(а):

Поправьте меня если не прав, но по-моему уравнение 4-й степени тригонометрически не решабельно. Есть и другие формулы четверного угла, под которые замену подобрать тоже нереально. И на math.stackexchange.com ничего кроме этого не находится.

судя по высказываниям котенка гав, все решается легко через косинус и это уровень школьный

Цитата:

Если я все вам разжую - это будет полное решение простой учебной задачи.

но кроме этого и ссылки на решение кубического уравнения, сообщить не соблаговолил.

а так хотелось ссылок и помощи у экспертов по теме "решение уравнения 4 степени через тригонометрию"

[kotenok gav]

Да, я ошибся.

[verywell]

вернемся все таки к теме.

Смотрите есть уравнение $x^4+x^2+x+1=0$ и $x^4+x^2-x+1=0$

Резольвента этих двух уравнений совпадает до знака и равна $y^3+4y^2-12y+(-8)=0$

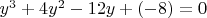
Получается "двоякость" которую надо как то определить.

Для всех вещественных коэффициентов исходного уравнения 4 степени можно найти методику определения какой знак брать.
Но у меня вызывает вопрос анализа знака, когда исходное уравнение имеет комплексные коэффициенты.

Как узнать например что коэффициент при x, имеет тот или иной знак, если как мы знаем что уравнение резольвенты будет одинакова, а другие коэффициенты уравнения 4 степени комплексные?

Совет, подставить корень в уравнение 4 степени и проверить истинность, идея замечательная, но вдруг кто то знает другой критерий?

[Someone]

verywell в сообщении #1378661 писал(а):

Но у меня вызывает вопрос анализа знака, когда исходное уравнение имеет комплексные коэффициенты.

Э-э-э… А что такое знак комплексного числа?

[Heart-Shaped Glasses]

verywell в сообщении #1378483 писал(а):

извините, а доказано ли что общее уравнение 4 степени, можно привести к биквадратному?
есть какая либо информация по этому вопросу?

Если посмотреть на корни биквадратного уравнения и немного подумать, то ответ очевиден.

[Someone]

С помощью дробно-линейной подстановки можно попробовать. Что-нибудь типа $x=\frac{ay+b}{y+1}$. Но там такая система уравнений получается…

[TR63]

verywell в сообщении #1378661 писал(а):

Резольвента этих двух уравнений совпадает до знака и равна $y^3+4y^2-12y+(-8)=0$

Это не резольвента двух уравнений:

verywell в сообщении #1378661 писал(а):

$x^4+x^2+x+1=0$ и $x^4+x^2-x+1=0$

verywell в сообщении #1378661 писал(а):

Для всех вещественных коэффициентов исходного уравнения 4 степени можно найти методику определения какой знак брать.

Для комплексных коэффициентов в форме $a+bi$ можно многочлен представить как сумму двух многочленов $f=P(x)+Q(x)i$ и решать раздельно два уравнения уже с действительными коэффициентами.

[mihiv]

Можно свести решение уравнения 4-й степени к решению пары квадратных уравнений, и тут, по-моему, вопроса о выборе знаков не возникает. Разложим полином 4-й степени на множители:

$$x^4+px^2+qx+r=(x^2+ax+b_1)(x^2-ax+b_2)$$

Для определения коэффициентов получаем систему уравнений:

$$\begin {cases}b_1+b_2=a^2+p\\b_2-b_1=\fraq qa\\b_1b_2=r\end {cases}$$

Из системы получаем, что $t=a^2$ удовлетворяет уравнению:

$$t^3+2pt^2+(p^2-4r)t-q^2=0\eqno (1)$$

Взяв любое значение $a$, полученное из уравнения (1), находим коэффициенты $b_1,b_2$ и решаем пару квадратных уравнений. В результате получим все 4 корня уравнения 4-й степени.

[TR63]

mihiv в сообщении #1378991 писал(а):

по-моему, вопроса о выборе знаков не возникает.

mihiv в сообщении #1378991 писал(а):

В результате получим все 4 корня уравнения 4-й степени.

В результате получим более четырёх корней и встанет проблема, какие четыре из них выбрать, чтобы выполнялось условие: $b_1b_2=r$. Или надо доказать, что это условие всегда выполняется (если доказать трудно, рассмотреть пример). В общем этот момент не ясен.

mihiv, Вашу формулу $(1)$ можно вывести ещё двумя способами. Но всё равно остаётся проблема выбора подходящих корней.

[mihiv]

Вкралась опечатка. Второе уравнение должно быть: $b_2-b_1=\frac qa$.

Из первых двух уравнений $b_1=\frac 12\left (a^2+p-\frac qa\right ), b_2=\frac 12\left (a^2+p+\frac qa\right )$. Подставляя $b_1, b_2$ в третье уравнение получаем:

$$\frac 14\left (\left (a+p\right )^2-\frac {q^2}{a^2}\right )=r,$$

а это и есть уравнение (1). Так что условие $b_1b_2=r$ автоматически выполнено. И теперь с помощью любого значения $a$, полученного из уравнения (1), мы получим все 4 корня исходного уравнения. Разные значения $a$ будут давать те же самые корни, но в другом порядке.

[TR63]

mihiv в сообщении #1379079 писал(а):

получаем:

$$\frac 14\left (\left (a+p\right )^2-\frac {q^2}{a^2}\right )=r,$$

а это и есть уравнение (1).

Это так всегда? У Вас получается одно уравнение четвёртой степени, другое шестой.

[mihiv]

TR63 в сообщении #1379116 писал(а):

У Вас получается одно уравнение четвёртой степени, другое шестой.

Исходный полином 4-й степени раскладываем в произведение двух полиномов 2-й степени: $P(x)=P_1(x)P_2(x)$. Полином $P_1(x)$ можно выбрать шестью различными способами ($C_4^2=6)$: $P_1(x)=(x-x_1)(x-x_2), P_1(x)=(x-x_1)(x-x_3)\dots $ и т.д.$x_i (i=1,\dots 4)$ -корни полинома 4-й степени. Каждое из 6 значений $a$, полученных из уравнения (1), соответствует определенному выбору полинома $P_1(x)$.

[Someone]

mihiv в сообщении #1379079 писал(а):

$$\frac 14\left (\left (a+p\right )^2-\frac {q^2}{a^2}\right )=r,$$

Явная опечатка: должно быть

$$\frac 14\left((a^2+p)^2-\frac{q^2}{a^2}\right)=r.$$