Я боюсь это уведёт нас в сторону, но вы упомянули двойственную задачу: найти стратегию с минимальным числом совпадений. Я думаю что это более сложная задача. Например: для "максимальной" задачи всегда находились симметричные решения, для "минимальной" это не так.
Но для двойственной задачи ("xor-дракона", когда принцессы должны выбрать разные исходы их бросков, чтобы спастись), похоже, тот же предел для вероятности; по крайней мере, для

это так. Вычислительная трудность для несимметричных стратегий растет с

до

, для маленьких

все еще обозримо; хочу попробовать, ну, наверное, уже ближе к следующим выходным.
То есть это все-таки оценка снизу
Нет, я имел в виду, что, скорее всего, это наилучшие стратегии, правда, доказывать, как выше предлагает
slavav не пытался, ограничился наглядными соображениями "вот четыре блока для задачи меньшего размера, вот внешний контур, вот "крест" посередине"...
-- 18.02.2019, 01:12 --(эксельное баловство с картинкой  )
)
Симметричная стратегия для

:
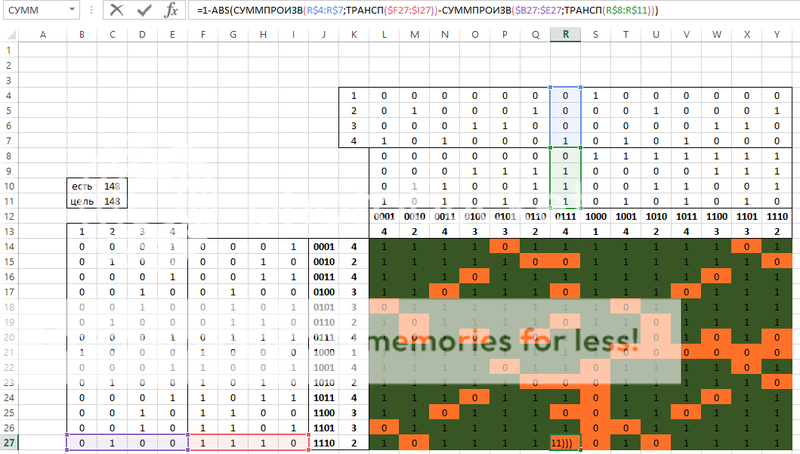
Из правого нижнего угла подбирается дракон, косичка одной из принцесс уже в его пасти; голова другой принцессы (с косичкой) - в левой части картинки