Задача по оптимизации операций (экстремальная задача).

[IvakhaAI]

Проверить, является ли точка x=(0;2) решением задачи
f($x)=$x_{1}+x_{2}\to \min$(найти локальный минимум)
при условии $g_{1}(x)=x_{2} - x_{1}^2 - 2 = 0$

Я написал функцию ЛаГранжа
$L=\lambda_{0}(x_{1}+x_{2})+\lambda_{1}(x_{2} - x_{1}^2 - 2)=0$

Я взял производные по $x_{1}$ и $x_{2}$ и еще взял доп. условие $g_{1}(x)$ получил систему из трех уравнений:

$\left\{ \begin{array}{rcl} \lambda_{0}-2\lambda_{1}x_{1}=0 \\ \lambda_{0}+\lambda_{1}x_{2}=0 \\ x_{2}-x_{1}^2-2=0 \\ \end{array} \right.$

И вот не уверен, что делать теперь. Если подставить точку (0;2) в эту систему, то лямбды будут равны нулю, и тогда о том является ли эта точка решением сказать будет нельзя. Если составить матрицу Гессе, то получится так, и что это мне дает не пойму...

$\begin{pmatrix} -2\lambda_{1}, 0 \\ 0, \lambda_{1} \\ \end{pmatrix}$

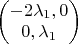
Спасибо за внимание

[Lia]

IvakhaAI
Формулы оформите нормально. Каждая должна начинаться со знака доллара, заканчиваться им и не содержать дополнительных долларов в середине. Формулы оформляем все.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.