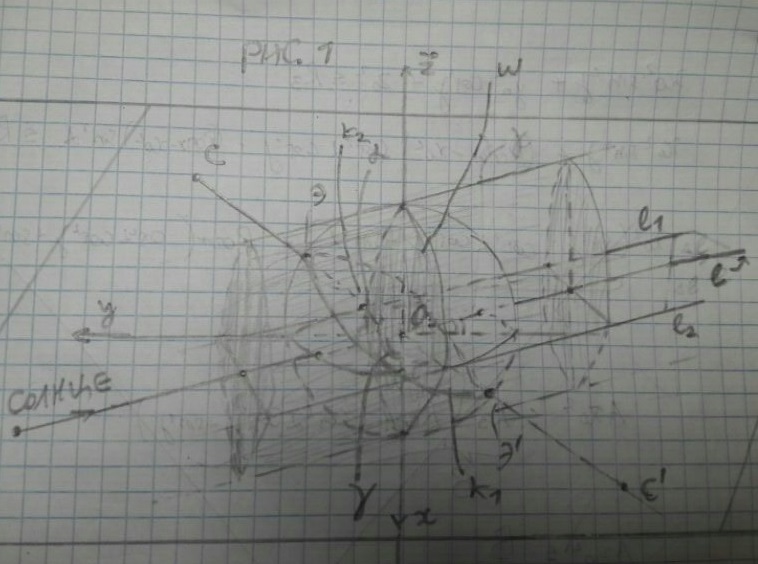
Послушал советы DimaM, напряг сегодня мозги и решил задачу так:
Рассмотрим цилиндр касающийся Земли и имеющий ось

, лежащую в орбитальной плоскости и проходящей через центр Земли. Пусть он пересекает Землю по окружности
![$\[\omega \]$ $\[\omega \]$](https://dxdy-04.korotkov.co.uk/f/f/c/4/fc496cc5389a96eb52b4729525b8ba7e82.png)
, а в прямых

касается проекции Земли на орбитальную плоскость в точках

. Обозначим положительный угол между

и

за
![$\[\gamma \]$ $\[\gamma \]$](https://dxdy-03.korotkov.co.uk/f/a/3/7/a376d37d6767ef4f9e7cc8ac4e58813e82.png)
. Ясно, что прямая

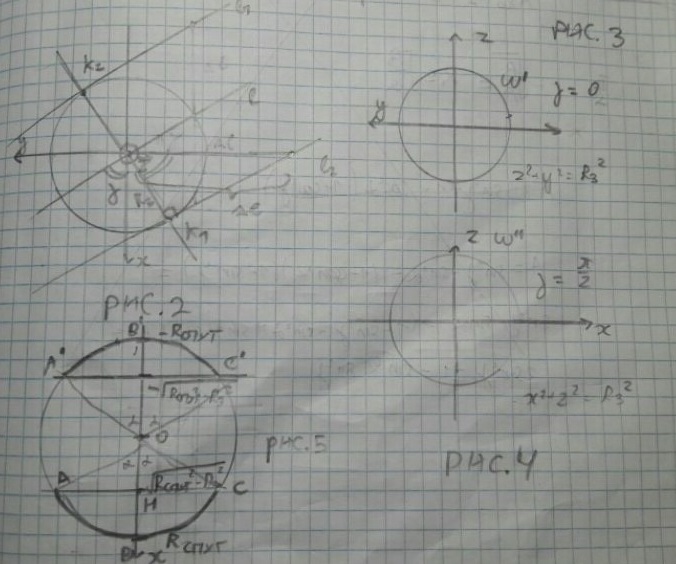
задается так(смотри рис.2 - проекция всей трехмерной картины на

):
![$$\[l{\text{ : }}y = x\tan \gamma \]$$ $$\[l{\text{ : }}y = x\tan \gamma \]$$](https://dxdy-03.korotkov.co.uk/f/2/f/c/2fc8bc00b020b5198a4dc0157835d22382.png)
Прямые

в ДСК выражаются так:
![$$\[\begin{gathered}
{l_1}{\text{ : }}y = x\tan \gamma + \Delta l \hfill \\
{l_2}{\text{ : }}y = x\tan \gamma - \Delta l \hfill \\
\end{gathered} \]$$ $$\[\begin{gathered}
{l_1}{\text{ : }}y = x\tan \gamma + \Delta l \hfill \\
{l_2}{\text{ : }}y = x\tan \gamma - \Delta l \hfill \\
\end{gathered} \]$$](https://dxdy-01.korotkov.co.uk/f/0/a/7/0a77fff19bc6199a7e983fd5c05061ee82.png)
Поскольку
![$\[\Delta l = \frac{{{R_{\text{З}}}}}{{\cos \gamma }}\]$ $\[\Delta l = \frac{{{R_{\text{З}}}}}{{\cos \gamma }}\]$](https://dxdy-01.korotkov.co.uk/f/8/4/e/84e93cb3fdbcd0bc72dc5857117e5cb982.png)
, то имеем окончательно:
![$$\[\begin{gathered}
Это система
{l_1}{\text{ : }}y = x\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \\
{l_2}{\text{ : }}y = x\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }}\\
\end{gathered} \]$$ $$\[\begin{gathered}
Это система
{l_1}{\text{ : }}y = x\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \\
{l_2}{\text{ : }}y = x\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }}\\
\end{gathered} \]$$](https://dxdy-01.korotkov.co.uk/f/4/1/7/417b7e8a2b1d7adbabcaf215c43bd0cd82.png)
Чтобы спутник

был в тени, необходимо, но не достаточно, чтобы он лежал внутри цилиндра, что равносильно тому, что проекция спутника на плоскость
![$\[\omega \]$ $\[\omega \]$](https://dxdy-04.korotkov.co.uk/f/f/c/4/fc496cc5389a96eb52b4729525b8ba7e82.png)
лежала внутри
![$\[\omega \]$ $\[\omega \]$](https://dxdy-04.korotkov.co.uk/f/f/c/4/fc496cc5389a96eb52b4729525b8ba7e82.png)
и что проекция спутника на орбитальную плоскость лежала внутри параллельных прямых

. Не достаточно потому, что тень существует только с одной стороны - за Землей, создающей тень. Условие расположения проекции

внутри

имеет вид:
![$$\[\left\{ \begin{gathered}
{y_0} \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }}\\
{y_0} \geqslant {x_0}\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \\
\end{gathered} \right.\]$$ $$\[\left\{ \begin{gathered}
{y_0} \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }}\\
{y_0} \geqslant {x_0}\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \\
\end{gathered} \right.\]$$](https://dxdy-01.korotkov.co.uk/f/8/1/e/81e58d404b19ab2eddac85459fd85ace82.png)
С учетом того, что
![$\[{y_0} = \pm \sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \]$ $\[{y_0} = \pm \sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \]$](https://dxdy-01.korotkov.co.uk/f/0/e/b/0ebbcd4d0de41e2ada318ed8a3e12a4982.png)
(до этого была опечатка -

вместо

), получим совокупность из систем:
![$$\[\left[ \begin{gathered}
\left\{ \begin{gathered}
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \geqslant {x_0}\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
- \sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant \frac{{{R_{\text{З}}}}}{{\cos \gamma }} - {x_0}\tan \gamma \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\]$$ $$\[\left[ \begin{gathered}
\left\{ \begin{gathered}
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \geqslant {x_0}\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
- \sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant \frac{{{R_{\text{З}}}}}{{\cos \gamma }} - {x_0}\tan \gamma \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\]$$](https://dxdy-04.korotkov.co.uk/f/3/b/e/3be6f13e8e9ce52bbad6b893cb923e5b82.png)
Допишем теперь условие, что проекция

лежит внутри
![$\[\omega \]$ $\[\omega \]$](https://dxdy-04.korotkov.co.uk/f/f/c/4/fc496cc5389a96eb52b4729525b8ba7e82.png)
. Уравнение этой окружности имеет вид:
![$$\[{x^2}{\sin ^2}\gamma + {y^2}{\cos ^2}\gamma + {z^2} = R_{\text{З}}^2\]$$ $$\[{x^2}{\sin ^2}\gamma + {y^2}{\cos ^2}\gamma + {z^2} = R_{\text{З}}^2\]$$](https://dxdy-02.korotkov.co.uk/f/1/2/0/120109ac8d84041fd77aa6e7626044dd82.png)
.
На рисунках 3 и 4 представлены частные случаи этой окружности при
![$\[\gamma \]=0$ $\[\gamma \]=0$](https://dxdy-03.korotkov.co.uk/f/a/6/e/a6ed38568a9dfd15a52afac32a4f088a82.png)
и
![$\[\gamma = \frac{\pi }{2}\]$ $\[\gamma = \frac{\pi }{2}\]$](https://dxdy-02.korotkov.co.uk/f/9/0/8/908f4e17b4690b920fb8bf90b07bcd7882.png)
что соответствует случаям, когда окружность вовсе не поворачивали и она расположилась на

и когда окружность повернули на

градусов и она попала на

. Подставляя в общее уравнение координаты спутника и записывая нестрогое неравенство, получим:
![$$\[x_0^2{\sin ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\cos ^2}\alpha {\cos ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\sin ^2}\alpha \leqslant R_{\text{З}}^2\]$$ $$\[x_0^2{\sin ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\cos ^2}\alpha {\cos ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\sin ^2}\alpha \leqslant R_{\text{З}}^2\]$$](https://dxdy-03.korotkov.co.uk/f/6/6/e/66e48c48d5c889fc1da6a41926408d4082.png)
Окончательно, критерий расположения спутника внутри цилиндра имеет вид:
![$$
\[\left\{ \begin{gathered}
x_0^2{\sin ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\cos ^2}\alpha {\cos ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\sin ^2}\alpha \leqslant R_{\text{З}}^2 \hfill \\
\left[ \begin{gathered}
\left\{ \begin{gathered}
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \geqslant {x_0}\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
- \sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant \frac{{{R_{\text{З}}}}}{{\cos \gamma }} - {x_0}\tan \gamma \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\]
$$ $$
\[\left\{ \begin{gathered}
x_0^2{\sin ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\cos ^2}\alpha {\cos ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\sin ^2}\alpha \leqslant R_{\text{З}}^2 \hfill \\
\left[ \begin{gathered}
\left\{ \begin{gathered}
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \geqslant {x_0}\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
- \sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant \frac{{{R_{\text{З}}}}}{{\cos \gamma }} - {x_0}\tan \gamma \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\]
$$](https://dxdy-04.korotkov.co.uk/f/b/4/a/b4a823cdbca6c344631930dbe526dc4082.png)
Это система с переменной

и параметром
![$\[\gamma \]$ $\[\gamma \]$](https://dxdy-03.korotkov.co.uk/f/a/3/7/a376d37d6767ef4f9e7cc8ac4e58813e82.png)
. Все остальные величины заданы:

км,

км,
![$\[\alpha = 23,44^\circ \]$ $\[\alpha = 23,44^\circ \]$](https://dxdy-01.korotkov.co.uk/f/8/1/6/816c8d5e9ad9ed2ac3df5b81741d594d82.png)
.
В изначальной задаче требуется найти максимальную длительность освещения и, наоборот, нахождения в тени спутника за период(1 сутки). Длительность эта зависит от угла
![$\[\gamma \]$ $\[\gamma \]$](https://dxdy-03.korotkov.co.uk/f/a/3/7/a376d37d6767ef4f9e7cc8ac4e58813e82.png)
. Найдя промежуток значений

из системы,мы найдем участок орбиты на которых спутник находится внутри цилиндра.Тогда сможем понять, сколько времени спутник тратит на прохождение этого участка, ведь мы знаем, что спутник проходит всю орбиту за сутки и движется с постоянной скоростью, следовательно отношение длины участка к длине орбиты, умноженное на сутки есть время, за сутки, когда спутник находится внутри цилиндра.
Здесь есть 2 проблемы. Во-первых, систему решить аналитически мне не удалось. Во-вторых, как я уже говорил, из того, что спутник лежит внутри цилиндра не следует, что он в тени, так что часть полученного из системы промежутка нужно будет отбросить. Дальше я рассуждал как физик:
1) Рассмотрю случай
![$\[\gamma = \frac{\pi }{2}\]$ $\[\gamma = \frac{\pi }{2}\]$](https://dxdy-02.korotkov.co.uk/f/9/0/8/908f4e17b4690b920fb8bf90b07bcd7882.png)
, рис. 4.
Докажу, что в этом случае спутник будет всегда будет освещен. Уравнение
![$$\[x_0^2{\sin ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\cos ^2}\alpha {\cos ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\sin ^2}\alpha \leqslant R_{\text{З}}^2\]$$ $$\[x_0^2{\sin ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\cos ^2}\alpha {\cos ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\sin ^2}\alpha \leqslant R_{\text{З}}^2\]$$](https://dxdy-03.korotkov.co.uk/f/6/6/e/66e48c48d5c889fc1da6a41926408d4082.png)
в этом случае можно записать так:
![$$\[x_0^2 + z_0^2 \leqslant R_{\text{З}}^2\]$$ $$\[x_0^2 + z_0^2 \leqslant R_{\text{З}}^2\]$$](https://dxdy-04.korotkov.co.uk/f/b/8/b/b8bb1f5441bce2cf599d81d89ac598a482.png)
Из него следует, что
![$$\[{x_0} \in \left[ { - {R_{\text{З}}};{R_{\text{З}}}} \right]\]$$ $$\[{x_0} \in \left[ { - {R_{\text{З}}};{R_{\text{З}}}} \right]\]$$](https://dxdy-04.korotkov.co.uk/f/b/e/3/be3cb4d625d8f54679a62a6bf82e2e9a82.png)
.
Из этого следует, что модуль минимального значения
![$\[\left| {{z_{0\min }}} \right|\]$ $\[\left| {{z_{0\min }}} \right|\]$](https://dxdy-04.korotkov.co.uk/f/3/7/1/3713109221aae6630734be96f3d24f2f82.png)
третьей координаты спутника можно оценить так
![$\[\left| {{z_{0\min }}} \right| \geqslant \sqrt {R_{\text{З}}^2 - x_0^2} \cos \alpha = \sqrt {{{35786}^2} - {{6380}^2}} \cos 23,44^\circ \approx 32570 > 6380\]$ $\[\left| {{z_{0\min }}} \right| \geqslant \sqrt {R_{\text{З}}^2 - x_0^2} \cos \alpha = \sqrt {{{35786}^2} - {{6380}^2}} \cos 23,44^\circ \approx 32570 > 6380\]$](https://dxdy-02.korotkov.co.uk/f/9/b/f/9bf97a023b6073f3e6bf329c46c3215582.png)
так что спутник заведомо не проецируется в плоскости
![$\[\omega \]$ $\[\omega \]$](https://dxdy-04.korotkov.co.uk/f/f/c/4/fc496cc5389a96eb52b4729525b8ba7e82.png)
внутрь окружности
![$\[\omega \]$ $\[\omega \]$](https://dxdy-04.korotkov.co.uk/f/f/c/4/fc496cc5389a96eb52b4729525b8ba7e82.png)
, значит спутник всегда будет снаружи цилиндра. Поэтому максимальная длительность освещения спутника за сутки равна суткам.
2) Рассмотрю случай
![$\[\gamma \]=0$ $\[\gamma \]=0$](https://dxdy-03.korotkov.co.uk/f/a/6/e/a6ed38568a9dfd15a52afac32a4f088a82.png)
. Как мне показалось, в этом случае достигается максимум длительности пребывания спутника в тени. Доказать я это не смог, но я отталкивался от того, что в данном случае цилиндр направлен на орбиту спутника "в лоб", то есть плоскость спутника перпендикулярная плоскости основания цилиндра. В данном случае картина происходящего весьма симметрична, и я посчитал, что в этом случае будет максимум. Обосновать строго не могу, надеюсь форумчане помогут.
Итак, если
![$\[\gamma \]=0$ $\[\gamma \]=0$](https://dxdy-03.korotkov.co.uk/f/a/6/e/a6ed38568a9dfd15a52afac32a4f088a82.png)
, то система
![$$
\[\left\{ \begin{gathered}
x_0^2{\sin ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\cos ^2}\alpha {\cos ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\sin ^2}\alpha \leqslant R_{\text{З}}^2 \hfill \\
\left[ \begin{gathered}
\left\{ \begin{gathered}
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \geqslant {x_0}\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
- \sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant \frac{{{R_{\text{З}}}}}{{\cos \gamma }} - {x_0}\tan \gamma \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\]
$$ $$
\[\left\{ \begin{gathered}
x_0^2{\sin ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\cos ^2}\alpha {\cos ^2}\gamma + \left( {R_{\text{Спут}}^2 - x_0^2} \right){\sin ^2}\alpha \leqslant R_{\text{З}}^2 \hfill \\
\left[ \begin{gathered}
\left\{ \begin{gathered}
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \geqslant {x_0}\tan \gamma - \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\end{gathered} \right. \hfill \\
\left\{ \begin{gathered}
- \sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant {x_0}\tan \gamma + \frac{{{R_{\text{З}}}}}{{\cos \gamma }} \hfill \\
\sqrt {R_{\text{Спут}}^2 - x_0^2} \cos \alpha \leqslant \frac{{{R_{\text{З}}}}}{{\cos \gamma }} - {x_0}\tan \gamma \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right. \hfill \\
\end{gathered} \right.\]
$$](https://dxdy-04.korotkov.co.uk/f/b/4/a/b4a823cdbca6c344631930dbe526dc4082.png)
равносильна
![$$\[{x_0} \in \left[ { - {R_{\text{Спут}}}; - \sqrt {R_{\text{Спут}}^2 - R_{\text{З}}^2} } \right] \cup \left[ {\sqrt {R_{\text{Спут}}^2 - R_{\text{З}}^2} ;{R_{\text{Спут}}}} \right]\]$$ $$\[{x_0} \in \left[ { - {R_{\text{Спут}}}; - \sqrt {R_{\text{Спут}}^2 - R_{\text{З}}^2} } \right] \cup \left[ {\sqrt {R_{\text{Спут}}^2 - R_{\text{З}}^2} ;{R_{\text{Спут}}}} \right]\]$$](https://dxdy-02.korotkov.co.uk/f/d/d/5/dd5067b48c179be819eb081f1aa0aa3382.png)
Графически это решение показано на рисунке 5 - это вид на орбиту спутника сверху. А теперь замечаем, что дуга

соответствует случаю, когда спутник расположен внутри цилиндра и освещен, так что этот промежуток выкидывает и рассматриваем дугу

. Ее длина

равна:
![$$\[{l_{{A_1}{B_1}{C_1}}} = 2\alpha {R_{\text{Спут}}} = 2\arcsin \left( {1 - \sqrt {1 - {{\left( {\frac{{{R_{\text{З}}}}}{{{R_{\text{Спут}}}}}} \right)}^2}} } \right){R_{\text{Спут}}}\]$$ $$\[{l_{{A_1}{B_1}{C_1}}} = 2\alpha {R_{\text{Спут}}} = 2\arcsin \left( {1 - \sqrt {1 - {{\left( {\frac{{{R_{\text{З}}}}}{{{R_{\text{Спут}}}}}} \right)}^2}} } \right){R_{\text{Спут}}}\]$$](https://dxdy-03.korotkov.co.uk/f/2/d/1/2d14d8cc644a4c024890d3a88a89843582.png)
, значит искомое время

равно
 -- 25.11.2018, 21:40 --
-- 25.11.2018, 21:40 --Вот такие вот дела.