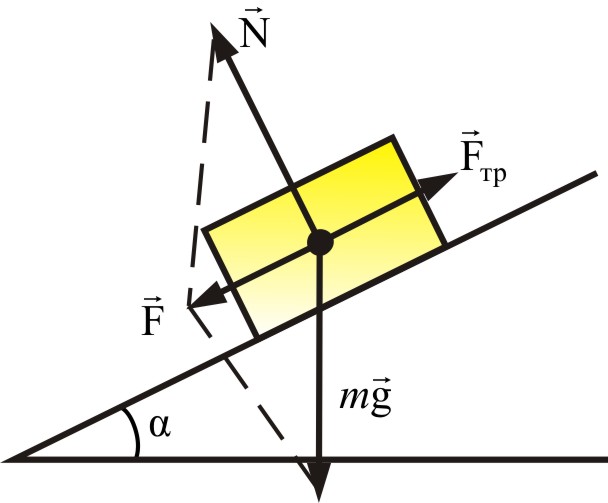
Тело движется по наклонной плоскости которая вращаеться

[fanat155]

Тело движется по наклонной плоскости у которой изменяется угол
Ускорение задано формулой $a=9.81\cdot( \sin({ \alpha+ \omega\cdot t })- 0.3\cdot \cos({ \alpha + \omega\cdot t }))$

где $\alpha = - 0.192 $ - первоначальный угол задан в радианах и изменяется.

$\omega$ = 0.052 - угловая скорость,она постоянна.


далее чтоб найти скорость я интегрирую
$\int\limits_{t_1}^{t_2} -9.81\cdot(\sin({ \alpha + \omega \cdot t }) - 0.3\cdot \cos({ \alpha+ \omega \cdot t }))dt=\frac{ -9.81 }{ \omega } \cdot((\cos({ \alpha+ \omega \cdot t_2}) -\cos({ \alpha+ \omega \cdot t_1 }) )+0.3\cdot(\sin({ \alpha\cdot\omega \cdot t_2})-\sin({ \alpha + \omega \cdot t_1 })))=23.372$

Проверяю площадью по графиком ускорения в автокаде скорость сходится.
Потом чтоб найти перемещения опять интегрирую

$\int\limits_{t_1}^{t_2}\frac{ -9.81}{ \omega } \cdot(\cos({ \alpha + \omega \cdot t })+ 0.3\cdot \sin({ \alpha+\omega \cdot t }))dt=\frac{ -9.81 }{ \omega ^{2} } \cdot(\sin({ \alpha + \omega \cdot t_2 })-\sin({ \alpha + \omega \cdot t_1 } ) -0.3\cdot(\cos({ \alpha + \omega \cdot t_2 })-\cos({ \alpha + \omega \cdot t_1 })))=1770$

А вот ускорения не сходиться должно быть 74.345

Временной интервал

$t_1 = 9.23$

$t_2 = 18.66$

Где ошибка не знаю уже голову себе сломал.В учебниках и задачника простые задачи где наклон не меняется.А такой нету(((

Формулировка задачи надо найти путь движения бруска по наклонной плоскости!
Представлен рисунок

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (посмотрите, как набираются нижние индексы; краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- фактически отсутствует формулировка задачи, поэтому непонятно, что вы делаете и зачем.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.