А вот как теперь доказать, что...
Можно воспользоваться тем известным фактом, что треугольное число (сумма натурального ряда) кроме
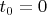
и

не может быть степенью целого с натуральным показателем

. Вернемся к началу.

Подставляя первое во второе, получаем

или

.

Выше у Вас доказано что

четно, и очень хорошо. Значит все скобочки в последнем равенстве суть нечетные квадраты, и можно записать

, где

- вз. простые разной четности. Тогда

Без потери общности можно назначить

откуда

(

вз. просты,

нечетно). Тогда

Основания равных квадратов должны дать

в сумме или в разности. В последнем случае, решая уравнение

, получаем

и


под радикалом. Остается

.

Значит

есть треугольное число, т.е.

Соответственно


Отсюда следуют оба ненулевых решения, и только они. Мутно, но верно. Доказать более общее утверждение
... что нетривиальных решений уравнения

всего два:

и

таким способом конечно не выйдет.