Эта тема является продолжением темы об асимптотической независимости слагаемых сумматорных арифметических функций Мертенса и Лиувилля. Но я бы просил модераторов не объединять темы, так как обычно более одной страницы не читают, а из старой темы мне потребуется только одна оценка, которую я здесь приведу.
Я уже писал об оценках функции Мертенса, но делал это с позиции вероятностных методов. В данной теме будут использоваться только точные методы: аналитические и элементарные.
Предметом обсуждения в данной теме является правильность доказательств указанных теорем. Буду благодарен за замечания и предложения.
В дальнейшем я буду говорить о минимальном порядке роста функции, поэтому поясню.
Напомню, что если

- две неограниченно возрастающие функции от вещественной переменной

и

и существуют два положительных числа

, таких что

для всех

, то пишут

и говорят, что порядок роста

равен

.
Примеры:

. Мы видим, что одна и та же функция может иметь различные порядки роста. Поэтому введем минимальный порядок роста, который станет ясен из примера.
Пусть имеется функция

, которая имеет, например, порядок роста

, что соответствует неравенству

, где

- постоянная. Естественно для

выполняется неравенство

. Если для

не выполняется неравенство

, то минимальный порядок роста

равен

.
В дальнейшем под порядком роста функции я буду понимать минимальный порядок роста. На это понятие меня навела многочисленная переписка с заслуженным участником форума
ex-math, за что я ему благодарен.
Теорема 1
Порядки роста функции Мертенса
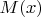
и ее среднего значения

совпадают.
Доказательство
Известна формула для функции Мертенса через теорему о вычетах:

,
где

-

-ый нетривиальный ноль дзета функции Римана.
Формула доказана при предположении справедливости гипотезы Римана и отсутствия кратности нетривиальных нулей дзета функции Римана.
В работе K.M. Bartz "On some complex explisit formulae connected with Mobius function." доказана аналогичная формула для
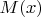
только без предположения о выполнении гипотезы Римана и отсутствия кратности нетривиальных нулей дзета функции Римана.
Рассмотрим эту формулу. Постоянная (-2) и второй знакочередующийся ряд по степеням

c малыми коэффициентами, который стремится к нулю, не влияют на асимптотику функции Мертенса.
На асимптотику функции Мертенса влияет только первый ряд:

, (1)
где

-

-ый нетривиальный ноль дзета функции Римана.
Среднее значение функции Мертенса получается интегрированием данной формулы для функции Мертенса и делением ее на

:

.(2)
На основании (2)

включает в себя постоянную (-2), знакочередующийся ряд по степеням

c малыми коэффициентами, стремяшейся к нулю, которые не влияют на асимптотику функции Мертенса, а также ряд по нетривиальным нулям дзета функции Римана, который влияет на асимптотику

:

,
который отличается от (1) только коэффициентами при

.
Ряд

- расходится, поэтому интегрировать его почленно нельзя.
Поэтому используется метод математической индукции.
Для первого нетривиального нуля

имеем:

.
Предположим, что соотношение выполняется для

первых нетривиальных нулей:

т.е:

.
Тогда получим для первых

нетривиальных нулей


.
Это значит, что утверждение верно для всех нетривиальных нулей:

.
Следовательно, порядки роста
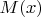
и

совпадают.
Теорема 2
Порядок роста функции Мертенса равен:

,(3)
где

- малое положительное число.
Доказательство
В работе Й.Кубилюс "Вероятностные методы в теории чисел" показано, что почти всюду для отклонения арифметической функции

от своего среднего значения

выполняется соотношение:

, (4)
где

- любая медленно растущая функция,

- стандартное отклонение.
Функция

обладает следующими свойствами:
1.

- является монотонной возрастающей функцией, начиная с некоторого

.
2.

.
3.

. (5)
Мы также рассмотрим случай:

, (6)
чтобы исследовать все случаи.
В случае (4) для порядка

справедливо соотношение:

. (7)
В теме
topic128802.html было доказано, что порядок стандартного отклонения функции Мертенса равен:

. (8)
Из (7) и (8) для функции Мертенса получаем:

. (9)
На основании (9) порядок функции
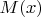
определяется максимум из порядков

и функций вида

для любых

.
На основании Теоремы 1 порядок функции Мертенса равен

.
Таким образом, на основании (9) порядок

больше порядка всех функций вида

для любой

.
Учитывая свойство (5) порядок роста

равен:

. (10)
На основании Теоремы 1 порядок роста функции Мертенса равен порядку

поэтому на основании (10):

, (11)
что соответствует эквивалентной формулировке гипотезы Римана.
Для случая (6), когда порядки роста функций

равны, то порядок отклонения равен:

. (12)
Но для случая (6):

для любой

. (13)
Поэтому на основании (5) и (13) порядок роста

и
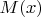
равен:

, (14)
что также соответствует эквивалентной формулировке гипотезы Римана.