Необходимо определить диаметр/радиус окружности (черного цвета на изображении), чтобы можно было на этой окружности разместить к примеру 11 окружностей красного цвета.
Окружность, даже красная -- она большая. Что в точности означают слова "расположить её на чёрной окружности"?
Если расположить надо их центры, то предыдущая картинка от
wrest исчерпывает вопрос: в треугольнике
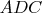
(например) маленький катет -- это заданный радиус, искомый радиус -- это гипотенуза, и противолежащий угол известен.