уравнение многомерной плоскости

[OlgaD]

Пытаюсь с нуля разобраться в теории многомерных плоскостей.
Очень нужна теория по вопросу: составить общее уравнение плоскости, минимальной размерности, содержащей данные две плоскости(похоже на topic58444.html). Где можно почитать об этом?

[arseniiv]

Тут несколько вопросов сначала:

1. Какие у вас подпространства, линейные (проходят через ноль) или аффинные?
1a. Понятен ли линейный случай, если аффинные?
2. Какое требуется уравнение? Неизвестно какое или специфическое (параметрическое, система линейных, что-нибудь со скалярными или внешними произведениями etc.)?

-- Вт май 15, 2018 00:06:01 --

Если что, параметрическое видится самым простым (потому что это, в сущности, и не уравнение), стоит начинать с него.

[OlgaD]

Задача звучит так: Составить общее уравнение плоскости минимальной размерности, которой принадлежат одновременно плоскость, проходящая через точку $A(2,4,-4,5)$ в направлении подпространства с базисом $a_1=(1,2,-4,3),a_2=(4,-1,-1,3),$ и плоскость с общим уравнением $2x_3-x_2-3x_1+x_4+3=0;\;2x_4-2x_2-x_3-x_1+1=0.$


Я нашла базис направляющего подпространства второй плоскости $b_1=(1,-1,1,0),b_2=(0,1,0,1)$ и точку на ней, точку $B(1,0,0,0).$ Ранг матрицы из векторов $a_1,a_2,b_1,b_2,AB$ равен 3, но куда двигаться дальше я не знаю, так как раньше такие задачи не решала.

[arseniiv]

Значит, аффинные, а вот какое уравнение они хотят, так и не ясно. Видимо, ту же линейную систему, которая называется тут просто «уравнение».

Так, ну тогда, в соответствии с вопросом 1а, смогли бы вы решить упрощённую задачу

Составить СЛУ подпространства минимальной размерности, которому принадлежат одновременно и подпространство с базисом $a_1=(1,2,-4,3),a_2=(4,-1,-1,3),$ и подпространство, заданное системой $2x_3-x_2-3x_1+x_4=0;\;2x_4-2x_2-x_3-x_1=0.$

?

UPD: Ага, ввиду продвижений вопрос снимается.

-- Вт май 15, 2018 00:15:29 --

Ага, дописали, сейчас прочту.

-- Вт май 15, 2018 00:42:38 --

OlgaD в сообщении #1312381 писал(а):

Я нашла базис направляющего подпространства второй плоскости $b_1=(1,-1,1,0),b_2=(0,1,0,1)$ и точку на ней, точку $B(1,0,0,0).$ Ранг матрицы из векторов $a_1,a_2,b_1,b_2,AB$ равен 3, но куда двигаться дальше я не знаю, так как раньше такие задачи не решала.

Прекрасно. Теперь если вы выделите из этих пяти векторов три линейно независимых, можно будет задать подпространство параметрически. 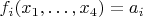Но раз нам нужно не это, надо взять наибольшее число линейно независимых линейных форм $f_i$ (здесь одну штуку — пространство четырёхмерно, вектора три, больше одной не влезет), обнуляющихся на каждом из этих векторов и найти, какому $a_i$ они равны в $B$ (или $A$); $f_i(x_1,\ldots,x_4) = a_i$ и будет нужной системой.

-- Вт май 15, 2018 00:46:06 --

(Если умеете находить базис ортогоналного дополнения $A^\bot$ по базису $A$, можете сделать это. Просто когда скалярного произведения на пространстве нет, аналогичная конструкция, не требующая его, имеется с линейными формами.)

[OlgaD]

С линейными формами не совсем поняла. Можно поподробнее?

Правильно ли я поняла, мне надо найти только одну линейную форму?

[arseniiv]

Здесь одну, да. Если вы знакомы со скалярным произведением и ортогональным дополнением подпространства, можете забыть про формы, наверняка ваше пространство подразумевается евклидовым. Результирующее координатное уравнение получится таким же.

[OlgaD]

Я попробовала все-таки решить через линейные формы. В результате у меня получился ответ $x_1+x_2-x_4-1=0.$

Попробую проверить через ортогональное дополнение.

Система для нахождения ортогонального дополнения та же, что и для определения коэффициентов формы, так что будет то же.

[arseniiv]

OlgaD в сообщении #1312542 писал(а):

Система для нахождения ортогонального дополнения та же, что и для определения коэффициентов формы, так что будет то же.

Именно!