Конечные поля

[error420]

Задача:
Доказать, что неприводимый над полем $GF(q)$ многочлен степени $n$ остается неприводимым над его расширением $GF(q^{m}) , m > 1$ тогда и только тогда, когда $n$ и $m$ взаимно просты.

Решение:
Пусть $n = n' \cdot k$ и $m = m' \cdot k$ , где $НОД (m,n) = k , k>1$.
Тогда
$x^{q^{kn'm'}}-x =\prod\limits_{}^{}h(x)$ , где $h(x)$ - неприводимые многолчены над полем $Fq$ степень которых делит $kn'm'$, значит там есть наш неприводимый многочлен, который мы исследуем
с другой стороны
$x^{q^{kn'm'}}-x =x^{(q^{m})^{n'}} = \prod\limits_{}^{}h'(x)$ где $h'(x)$ - неприводимые многолчены над полем $Fq^{m}$ степень которых делит $n'$, а значит наш многолчен (который мы ислледуем) разложился на другие неприводимые над полем расширения, так как в равенстве справа многочленов степени n нет.

Для случая когда взаимнопростые $(n, m)$ доказать, что многочлен останется неприводимым не выходит

[vpb]

Не уверен, что Вы имеете достаточно знаний по алгебре (судя по предыдущим темам), но попробую написать.

Предположим, что $(m,n)=1$. Напомним такой факт: все подполя в $GF(p^l)$ --- это в точности поля вида $GF(p^s)$, причем $s\mid l$, и для каждого $s\mid l$ существует ровно одно подполе в $GF(p^l)$, изоморфное $GF(p^s)$.

Пусть $f(x)$ --- неприводимый над $F=GF(q)$ многочлен степени $n$. Пусть $E=GF(q^{mn})$, $K,L\subseteq E$ --- подполя порядков $q^n$, $q^m$ соответственно (такие подполя в $E$ единственны); и $F$ также представляем себе подполем в $E$.

Существует элемент $\alpha\in K$ такой, что $f(\alpha)=0$. Конечно, $\alpha$ порождает $K$ над $F$. Пусть $f(x)=f_1(x)\ldots f_r(x)$ --- разложение $f$ над $L$. Тогда $f(\alpha)=0$, откуда одно из $f_i(\alpha)$ равно нулю. Можно считать, что $i=1$. Нам надо показать, что на самом деле $f=f_1$. Имеем $[L(\alpha):L]\leq\deg f_1$ по общим свойствам расширений полей. 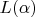Если $f\ne f_1$, то $\deg f_1<n$, откуда $[L(\alpha):L]<n$, и значит $L(\alpha)$ --- собственное подполе в $E$.
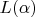
Однако $L(\alpha)\supseteq F(\alpha)=K$, откуда $L(\alpha)$ содержит оба подполя $L$ и $K$. Но единственное подполе в $E$, содержащее оба $L$ и $K$ --- это само $E$; противоречие. Значит, на самом деле $f=f_1$.

[error420]

vpb
Существует элемент $\alpha\in K$ такой, что $f(\alpha)=0$. Конечно, $\alpha$ порождает $K$ над $F$.
Это утверждение только в случае если наш многочлен помимо неприводимого, является еще и примитивным, что не обязательно.

Имеем $[L(\alpha):L]\leq\deg f_1$
Не знаком с этим обозначением, не расшифруете?

[nya]

После присоединения корня получится поле размера $p^n$ оно лежит в $p^m$ только когда $n$ делит $m$.

[error420]

nya
поле размера $p^n$ оно лежит в $p^m$ только когда $n$ делит $m$.
Этот факт мне известен, но к сожалению не является ключевым в решении этой задачи, так как одного этого не достаточно для формулировки утверждения из условия.

[nya]

к счастью достаточно, ну + ещё факт что любое конечное расширение конечного поля нормально, но это очевидно

[error420]

nya
В таком случае необходимы пояснения
Изначально не понял "после присоединеня корня получится поле"
Присоединение корня к чему? и Как из этой субстанции получается поле?

На счет нормального расширения - такого не было, погуглили, вроде с этим все понятно.

[vpb]

error420 в сообщении #1312169 писал(а):

помимо неприводимого, является еще и примитивным

Скажите, а что Вы имеете в виду под примитивным многочленом ? Я этот термин редко встречал, и в тех случаях, когда встречал, это, кажется, был синоним неприводимого.

[error420]

vpb
Неприводимый многочлен - многочлен который не раскладывается в произведение многочленов меньших степеней
Примитивный многочлен - неприводимый многочлен, корень которого является пораждающим элементов мультипликативной группы поля

[vpb]

error420 в сообщении #1312169 писал(а):

Имеем $[L(\alpha):L]\leq\deg f_1$
Не знаком с этим обозначением, не расшифруете

$\deg f$ --- степень многочлена. $[E:F]$ --- степень расширения $E/F$ (т.е. размерность $E$ как векторного пространства над $F$).

[error420]

vpb
Так многочлен $x^{3} + 1 является неприводимым над $Z_3$ но не является примитивным, так как его корень $x$ в четвертой степени будет давать единицу.

[nya]

error420
пусть $(m,n)=1$ рассмотри ромб
$GF(q) \subset GF(q^n) \subset GF(q^{nm})$
$GF(q) \subset GF(q^m) \subset GF(q^{nm})$
в $GF(q^n)$ у тебя $f$ расщепляется, выбери автоморфизм $\sigma \in Gal(GF(q^{nm})/GF(q))$ который оставляет $GF(q^m)$ на месте, он же будет крутить корни $f$ по циклу, а они все разные, поэтому если бы было что $f=gh$ в $GF(q^m)$ этот автоморфизм поменял бы корни $g$ и $h$ местами, оставив при этом на месте коэффициенты, а это невозможно.

-- 13.05.2018, 20:12 --

$\sigma(x) = x^{q^m}$ - автоморфизм фробениуса

[vpb]

error420 в сообщении #1312188 писал(а):

Так многочлен
$x^{3} + 1$ является неприводимым над $Z_3$

Нет, это не так, так как над $Z_3$ имеем $(x+1)^3=x^3+1$.

[error420]

vpb
Да я вроде понял доказательство, и вопрос примитивности не влияет, так как ключевое утверждение $L(\alpha)\supseteq K$ можно сделать исходя из природы $L(\alpha)$

-- 13.05.2018, 19:14 --

vpb
ошибся $x^{2} + 1$ имел ввиду
мощность мультипликативной группы 8, проверяем $x^4$ равен единице

-- 13.05.2018, 19:16 --

nya
Спасибо за помощь, но боюсь для Вашего доказательсвта, моя подготовка не достаточна. автоморфирзм фробениуса мне не знаком)

-- 13.05.2018, 20:06 --

vpb
Ан нет, немного осело и снова возникли вопросы
$L(\alpha)\supseteq K $ , не очень понял почему так вышло?

и $\alpha$ элемент поля $K$, каким образом мы пользуемся им в поле $L$

[vpb]

Я думаю, основная проблема состоит в том, что Вы недостаточно знаете, что такое расширения полей и т.д. Объяснять Вам это сейчас, что называется, "на колене" --- это будет безуспешно, и задача форума другая.
В связи с этим, хочу рекомендовать кое-какую литературу. С требуемыми сведениями можно познакомиться по одной из книг: либо
(а) А.И.Кострикин, Введение в алгебру, том 1, главы 4,5 + том 3, гл.5, параграфы 1,2
либо
(б) Б.Л.ван дер Варден, Алгебра, главы 1--3, затем параграфы 19--21, 27--33, 37--43.
(если вдруг что написано в одном из этих источников не очень хорошо, то хорошо написано в другом).
Также есть хорошая книга
(в) Л.А.Калужнин, Введение в общую алгебру. (первые 5 глав).