Кстати, энергетический подход полезен и для школьных задач типа той же бритвы.
Поверхностное натяжение

для прямой линии, и

для малого участка, и направлена вдоль поверхности перпендикулярно к линии. Эквивалентно это можно сформулировать как то, что с поверхностью связана энергия

так что когда мы пытаемся увеличить поверхность, то мы должны сообщить эту энергию.

Почему плавает бритва? Чтобы она утонула, её должна сверху покрыть вода. Площадь воды должна увеличиться на
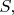
а энергия, соответственно, на

А откуда эта энергия может взяться? Выигрыш потенциальной энергии за счёт того, что бритва сместится вниз, равен

В первый момент уменьшение высоты очень мало́ (например, чтобы вода покрыла бритву, ей надо погрузиться на глубину порядка 1 мм), и выигрыш потенциальной энергии недостаточен, чтобы покрыть всю бритву плёнкой воды.
Будем мысленно увеличивать толщину бритвы (металлической пластины). Тогда при некоторой массе наступит момент, когда выигрыш потенциальной энергии достаточно велик, и пластина утонет.
Однако надо понимать, что здесь речь идёт о локальном барьере энергии. Если взять потенциальную энергию в сравнении с положением пластины на дне стакана, то она окажется очень велика - но затратить её на противодействие поверхностному натяжению уже невозможно. Надо рассматривать именно первый очень короткий участок погружения - в зависимости от жидкости, тела и других условий (температура, газы, поверхностно-активные вещества, вязкость) он может колебаться в районе миллиметров.
-- 02.05.2018 16:12:50 --Заодно уж можно добавить, что поверхностные явления - область, в которой все понять (пока) несколько затруднительно.
Пока человек читает Матвеева, добавлять это излишне. До затруднительных мест ему ещё далеко. Такие вещи, как угол смачивания, связь с парообразованием, ПАВ - достаточно хорошо изучены и описаны, и их ему ещё надолго хватит.