Про даму с собачкой: пусть дама гуляет вокруг церкви по (беговой) дорожке - окружности радиуса

. На поводке длины

у нее - собачка; к этой собачке веревочкой длины
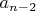
привязана собачка поменьше, и т.д. Пусть угловая скорость дамы равна

(шустрая такая дама), первой собачки -

, ..., предпоследней - равна 1, а последней - 0 (вмерла, видимо), поводки всегда натянуты. Показать, что за время

дохлую собачку эта компания ровно

раз
протащит вокруг церкви (так что соответствующее уравнение - с косинусами - будет иметь не менее

корней: столько раз она пересечет вертикаль

).
Решение. Дети говорят - дык, очевидно (если сумма длин веревочек меньше радиуса круга). Большие дети говорят: дык, приращение аргумента равно приращению аргумента главного слагаемого (вынесем его за скобку; в скобке останется единичка плюс что-то меньшее единицы; приращение аргумента скобки равно 0) ...
Про Ваши оценки (которые "дальше"): Вы оцениваете КВАДРАТЫ модулей функций, да? А что, квадрат суммы всегда меньше суммы квадратов?
Но у Вас - да, не такие условия на коэф-ты. Я прикидывал: если сделать преобразование Абеля ("дискретное интегрирование по частям"), заменив сумму произведений на сумму произведений "нарастающих сумм" и разностей, то, вроде, Ваше условие трансформируется в "дамособачкино". Может, это Вам поможет?
Но выглядит это как то слишком сложно, должно быть, я полагаю, что-то попроще...