Спасибо за ответы! Всё же попытаю счастье решить эту задачу)

вроде удовлетворяет условию.
Забыл пару важных деталей в условии.
Дано хаусдорфово
непустое регулярное топологическое пространство

. Известно, что оно является объединением двух своих подпространств, таких, что в каждом из них (например,

) для любой точки

существует такая её окрестность

, что
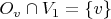
. Верно ли, что в пространстве

существует изолированная точка?
Итак, к какому выводу я пришёл, в том числе благодаря форумчанам

Оба подпространства состоят целиком из изолированных точек в своих топологиях. Предположим, что в

не существует изолированной точки. То есть, для каждой точки

любая её окрестность имеет со множеством

по крайней мере две точки пересечения: сама точка

и точка

. Заметим, что

и

не могут лежать в одном подпространстве (поскольку каждое из подпространств

состоят только из изолированных точек). Следовательно, если, например,

, то

...
Полагаю, что как-то нужно использовать тот факт, что пространство

- хаусдорфово (т.е. для любых двух различных точек существуют их непересекающиеся окрестности). Буду признателен, если кто-то подтолкнёт на правильный путь в доказательстве этого факта)