Здравствуйте!
Встретил матричные соотношения которые никак не могу уяснить для себя. Имеется матрица

размера
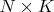
, столбцы которой представляют из себя векторы данных. Фильтр - ортогонализатор описывается матрицей

размера
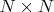
. Действие матрицы фильтра

на исходный набор данных

обладает следующим свойством:

(1)

То есть происходит ортогонализация исходного набора данных.
Затем вводится матрица

, так называемая матрица фильтра-биортогонализатора. Она обладает следующим свойством при действии на исходный набор данных

:

(2)

То есть происходит биортогонализация исходного набора данных.
Далее в источнике утверждается что проверить соотношения (2) непосредственно не составляет труда если выполняются соотношения (1). И тут я впал в ступор) Никак не получается доказать соотношения (2). Судя по всему я упускаю какие то матричные тожедства( Буду рад любой помощи!