Как посчитать интеграл нормального распределения?

[valery99]

Найти вероятность попадания в интервал от 1.6 до 3.6? Мы можем прекрасно посчитать на пк и будет 0.16. Можем посчитать с помощью таблицы функции Лапласа и будет 0.16. А можно ли мне определенный интеграл от плотности вероятности свести как-то к табличному без использования пк и готовой таблицы Лапласа или Гаусса? Я совершенно не пойму как это сделать? Нужно интегрировать по частям? Вообще как такие задачи можно решить?

математическое ожидание = 0, среднеквадратическое отклонение = 4.

[Dan B-Yallay]

valery99 в сообщении #1297219 писал(а):

А можно ли мне определенный интеграл от плотности вероятности свести как-то к табличному без использования пк и готовой таблицы Лапласа или Гаусса?

Неберущиеся интегралы

[Евгений Машеров]

Этот интеграл в элементарных функциях не выражается. Для его вычисления предложено несколько аппроксимаций.
https://en.wikipedia.org/wiki/Normal_di ... normal_CDF

[valery99]

Евгений Машеров в сообщении #1297222 писал(а):

Этот интеграл в элементарных функциях не выражается. Для его вычисления предложено несколько аппроксимаций.
https://en.wikipedia.org/wiki/Normal_di ... normal_CDF

А вот такой вариант? Только мы же должны пределы менять в определенном интеграле и в таблице значения даны для 0 или минус бесконечности в нижнем пределе. Или я чего-то не понимаю?

[Евгений Машеров]

Ну Вы же просили "без таблицы". А Ф(х) это "таблица". Ну, или программа, выдающая численную аппроксимацию.

[mihaild]

valery99 в сообщении #1297225 писал(а):

А вот такой вариант?

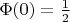
Вариант чего? $\Phi$ здесь - это ровно функция распределения, ее и нужно посчитать (точнее разность двух ее значений). В некоторых точках ее можно посчитать аналитически (например, $\Phi(0) = \frac{1}{2}$), но в остальных придется считать численно. Скорее всего в ваших точках она никак хорошо аналитически не выражается.

(а на вашей картинке (кстати, наберите формулу, пока не унесли в Карантин) в третьем равенстве забыли поменять пределы интегрирования...)

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.