найти для начала область однолистности просто для гиперболического синуса
Найдём область однолистности

.

имеет период

, поэтому можем взять горизонтальную полосу
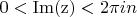
.
Это однолистность, для конформности ещё проверим равенство нулю производной:

при
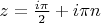
. Поэтому в качестве максимальной области конформности можем взять полосу
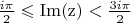
.
Далее берём композицию
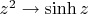
. Композиция конформных должна быть конформной, верно?
Максимальная область конформности для

верхняя полуплоскость. Надо в качестве итоговой области взять те точки верхней полуплоскости, которые переходят при возведении в квадрат в полосу
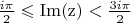
. Верно рассуждаю?
Но вот здесь и непонятно, как дальше. Единственная мысль

. И далее берем числа для которых
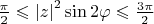
. Но какой-то ответ некрасивый. Что делать?