произведение объектов в конкретной категории

[beroal]

«Структура», конечно, понятие расплывчатое, поэтому я возьму конкретные примеры: алгебраические структуры и топологическое пространство. Как мне кажется, произведение этих структур строится по одной схеме, которую можно формализовать с помощью теории категорий, а именно, понятия конструкт (construct), которое есть частный случай понятия конкретная категория (concrete category). (Обозначения и определения взяты из книги в конце поста.)

Определение. Пусть $\mathrm{\mathbf{X}}$ есть категория. Конкретная категория над $\mathrm{\mathbf{X}}$ есть пара $(\mathrm{\mathbf{A}}, U)$, где $\mathrm{\mathbf{A}}$ есть категория и $U:\mathrm{\mathbf{A}}\to\mathrm{\mathbf{X}}$ есть строгий функтор. Конкретная категория над $\mathrm{\mathbf{Set}}$ называется конструктом. 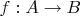Для объектов $A$ и $B$ категории $\mathrm{\mathbf{A}}$ будем говорить, что морфизм $g: U(A)\to U(B)$ есть $\mathrm{\mathbf{A}}$-морфизм типа $A\to B$, если существует морфизм $f: A\to B$ такой, что $g=U(f)$.

В моих примерах $\mathrm{\mathbf{A}}$ есть категория алгебраических структур или топологических пространств, $\mathrm{\mathbf{X}}$ есть $\mathrm{\mathbf{Set}}$, $\mathrm{\mathbf{A}}$-морфизм есть гомоморфизм или непрерывная функция соответственно.

Пусть $\bar{A}$ есть семейство объектов $\mathrm{\mathbf{A}}$. (То есть $\bar{A}$ есть функция, которая возвращает объект категории $\mathrm{\mathbf{A}}$.) Я полагаю, что, чтобы построить произведение $\bar{A}$, достаточно построить объект $A$ (алгебраическую структуру или топологическое пространство соответственно) такой, что $U(A)$ есть произведение $U\circ\bar{A}$, и доказать, что проекции есть $\mathrm{\mathbf{A}}$-морфизмы и произведение $\mathrm{\mathbf{A}}$-морфизмов есть $\mathrm{\mathbf{A}}$-морфизм. Не упустил ли я чего? Где об этом можно почитать? Я ожидал, что это будет в учебнике, полистал разделы «Concrete categories and concrete functors» (страница 61) и «Limits and colimits» (страница 193), но не нашёл ничего похожего.

Adámek, Jiří, Horst Herrlich, and George E. Strecker. Abstract and Concrete Categories: The Joy of Cats. FG KatMAT. University of Bremen, 12 Jan. 2004. Web. 29 Jan. 2018.

[arseniiv]

Так ведь произведения бесконечного множества объектов строятся точно так же как и конечного. Вот если нужна прямая сумма, всё сложнее (я открыл статью в nLab и ничего не понял кроме того, что у неё два обобщения, иногда не совпадающие).

[Chanzaa]

Но ведь конкретная категория может быть очень маленькой, разве нет? В ней может просто не иметься прообразов для универсальных set-стрелок. Например, рассмотрим вот такую категорию J с четырьмя объектами и четырьмя неединичными морфизмами.



В этой категории есть два конуса с вершинами в C и в D.
Ни один из конусов не является универсальным, как легко видеть.

Построим функтор U из J в Set:
объекты A и B отправим в какие-нибудь различные множества a и b,
объект C отправим в прямое произведение a на b,
объект D отправим в какое-нибудь другое множество,
стрелки из C отправим в канонические проекции,
стрелки из D - просто в какие-нибудь две функции.

Вроде как получится конструкт.
Объект C обладает всеми требуемыми свойствами, но не является произведением, т.к. не обладает универсальным свойством - в J нужной универсальной стрелки нет.

Я ничего не перепутал?

[beroal]

arseniiv в сообщении #1288975 писал(а):

Так ведь произведения бесконечного множества объектов строятся точно так же как и конечного.

Ну, я нигде не писал, что произведение конечно. По-моему, это не существенно в данном случае.

Chanzaa в сообщении #1289036 писал(а):

Объект C обладает всеми требуемыми свойствами, но не является произведением, т.к. не обладает универсальным свойством - в J нужной универсальной стрелки нет.

Я ничего не перепутал?

Обозначим морфизмы в вашем примере: $f: U(D)\to U(A)$ есть $\mathrm{\mathbf{J}}$-морфизм типа $D\to A$, $g: U(D)\to U(B)$ есть $\mathrm{\mathbf{J}}$-морфизм типа $D\to B$. Произведение $f$ и $g$ существует и имеет тип $U(D)\to U(C)$, но не является $\mathrm{\mathbf{J}}$-морфизмом типа $D\to C$ согласно определению $\mathrm{\mathbf{J}}$. Следующее требование вы упустили из виду в вашем примере:

beroal в сообщении #1288973 писал(а):

доказать, что… произведение $\mathrm{\mathbf{A}}$-морфизмов есть $\mathrm{\mathbf{A}}$-морфизм

[arseniiv]

beroal в сообщении #1289749 писал(а):

Ну, я нигде не писал, что произведение конечно.

Да уж, мне надо было подумать перед тем как писать не о том, извините.

[george66]

Это неверно в общем случае. Носитель произведения может быть не равен произведению носителей. Он равен для произведений групп, колец и любых других алгебраических систем, заданных аксиомами вида "равенство двух термов" (тождествами, таковы аксиомы ассоциативности, дистрибутивности и т.д.). Потому что в этом случае стирающий функтор имеет левый сопряжённый (выдающий по множеству свободную группу, кольцо и т.п.) и потому сохраняет произвдения (правый сопряжённый функтор всегда их сохраняет). Для более сложных алгебраических систем (каких-нибудь "групп без кручения") произведение может быть устроено сложнее, "наивное"произведение может быть "с кручением" и его надо как-то поправлять. Посмотрите в мат.энциклопедии статью "алгебраическая система".

[beroal]

george66 в сообщении #1289996 писал(а):

Это неверно в общем случае.

Начнём с этого: что именно не верно?

[george66]

Я понял вопрос так: чтобы построить произведение семейства объектов, необходимо и достаточно построить произведение их множеств-носителей и задать на нём подходящую структуру. Если строим произведение групп, берём произведение их множеств-носителей и на нём задаём структуру группы. Так вот, в общем случае носитель произведения не является произведением носителей. Для групп это так, потому что существуют свободные группы (и у стирающего функтора есть левый сопряжённый).

[beroal]

george66 в сообщении #1290101 писал(а):

Я понял вопрос так: чтобы построить произведение семейства объектов, необходимо и достаточно построить произведение их множеств-носителей и задать на нём подходящую структуру.

Видимо, в ваших контрпримерах не возможно задать подходящую структуру, вот и всё. Такую, какую я описал ниже.

beroal в сообщении #1288973 писал(а):

Я полагаю, что, чтобы построить произведение $\bar{A}$, достаточно построить объект $A$ (алгебраическую структуру или топологическое пространство соответственно) такой, что $U(A)$ есть произведение $U\circ\bar{A}$, и доказать, что проекции есть $\mathrm{\mathbf{A}}$-морфизмы и произведение $\mathrm{\mathbf{A}}$-морфизмов есть $\mathrm{\mathbf{A}}$-морфизм.

Речь не только об алгебраических структурах. Я не знаю, как оформить топологическое пространство в виде алгебраической структуры. Насколько я понимаю, фрейм не является полным аналогом топологического пространства. Поэтому и нужна теория категорий.

-- Sun Feb 11, 2018 20:51:58 --

george66 в сообщении #1289996 писал(а):

Для более сложных алгебраических систем (каких-нибудь "групп без кручения") произведение может быть устроено сложнее, "наивное"произведение может быть "с кручением" и его надо как-то поправлять.

А что это за контрпримеры? «Кручение» — это из алгебраической топологии?

[george66]

Не помню, я не алгебраист. Берутся группы, в которых то ли все элементы конечного порядка, то ли что-то в этом роде. Их произведение как групп может таким свойством не обладать, из него надо выбрать часть, состоящую из правильных элементов, она и будет произведением. Посмотрите в мат энциклопедии статью "произведение", там есть примеры.

[george66]

Вот пример в соседней теме
topic124801.html

[beroal]

george66 в сообщении #1291882 писал(а):

Посмотрите в мат энциклопедии

Я же не знаю, какую энциклопедию вы имеете в виду.

[george66]

Наберите "математическая энциклопедия"
http://gen.lib.rus.ec/