Синий -- квадратный корень из количество шагов.
"Границы" блуждания не даются этой функцией. Пусть случайные величины

,

,
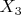
, … одинаково распределены, независимы, имеют математические ожидания

и дисперсии

. Обозначим

Последовательность

,

,

, … — дискретный случайный процесс с независимыми приращениями. "Границы" для последовательности

даются так называемым законом повторного логарифма:

Точное утверждение состоит в том, что при

случайный процесс с вероятностью

пересекает каждую из границ конечное число раз, а при

— бесконечное. Можно попробовать изобразить на графике эти границы при

. Но в вашем численном эксперименте для разных вероятностей выигрыша границы будут разными: они зависят от математического ожидания и дисперсии выигрыша в одной игре.
Если величина выигрыша задаётся правилом

то

,

.
Исправление. Виноват, выражение для границ написал неправильно. Исправил.
Мы все время говорим о том, что при равновероятных исходах, предыдущую их историю можно забыть, т.к. она не влияет на последующие исходы, и тогда, казалось бы, каждое пересечение нуля это для игрока как бы "перезапуск" игры с начала. Но нет.
Почему нет? Именно так и есть. Просто чем дольше продолжается игра, тем более редкие события реализуются. Поэтому понемногу величина отклонения

от

в среднем увеличивается.
Прошу прощения за кучу цитат, но иначе читателям придётся долго разыскивать, на какой вопрос я отвечаю.
Так не бывает. Сумма этих вероятностей не больше единицы.
Выигрыш - это прирост капитала игрока, а проигрыш - уменьшение
С какой, по-вашему, вероятностью, игрок может прирастить капитал при бесконечном количестве бросков монеты?
Это значит, что можно побрасывать монетку пока не будет получен выигрыш.
Тогда вероятность выигрыша равна единице.
Теперь вместо слова "выигрыш" ставим "проигрыш"...
Тогда вероятность тоже единица.
При такой интерпретации обсуждаемые события относятся к разным вероятностным пространствам, поэтому никаких утверждений типа "сумма вероятностей равна

" сделать нельзя. События только кажутся противоположными, но на самом деле таковыми не являются. Если мы останавливаем игру в тот момент, когда получим выигрыш, мы получим один набор элементарных исходов, а если в момент проигрыша — другой. У этих пространств даже нет общих элементов.
Другая возможная интерпретация состоит в том, что мы действительно реализуем бесконечную последовательность игр и хотим найти вероятность того, что предельный выигрыш будет положительным. Однако в таком случае никакого предельного выигрыша не будет: последовательность

с вероятностью

совершает хаотические колебания в постепенно неограниченно расширяющихся границах, бесконечно много раз меняя знак.
P.S.
wrest, Вы в какой программе моделируете игру? Насколько хорош там генератор псевдослучайных чисел?
Впрочем, в современных математических пакетах эти генераторы должны быть приемлемого качества. Просто меня немного насторожила
зелёная линия на втором графике. Но если Вы много раз прогоняли модель и выбрали самый "худший" вариант, то это нормально.