Неоднородная система линейных ДУ

[khammisha]

Добрый день! Помогите пожалуйста решить задачку по дифурам. Ниже привожу условие задачи и свои размышления:

Дана неоднородная система линейных уравнений, здесь \omega-вещественный параметр. Указать все значения параметра \omega, при которых система имеет:

а)решение, ограниченное при t \geqslant 0
б)решение, пересекающее ось OX счетное количество раз?

\frac{d x}{d t}=y+\sin{ \omega t}

\frac{d y}{d t}=-x

Как я решаю:
1)Решаю систему однородных уравнений вида:

\frac{d x}{d t}=y

\frac{d y}{d t}=-x

Собственные числа тут это \lambda = \pm i
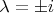
Получаю такие решения:
x=c_{2} \sin{t}+c_{1}\cos{t}
y=c_{2}\cos{t}-c_{1}\sin{t}

2)Затем нахожу частное решение, рассматривая случаи:
1) \omega^{2}=1 (чтобы комплексное число правой части являлось корнем характеристического многочлена)
2)\omega^{2} \ne 1 (чтобы не являлось)
3)\omega^{2}=0

Посмотрю для каких \omega решение будет существовать, а вот что дальше делать понятия не имею.
Как отсюда выполнить пункты а) и б) ?
В пункте б) я так понимаю необходимо чтобы решение было периодическим и ограниченным?
Буду рад любой помощи и подсказке.

[Pphantom]

Тема перемещена из форума «Помогите решить / разобраться (М)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы); теги math можно не расставлять вручную, они добавятся сами, но надо окружить каждую формулу долларами (или двойными долларами), причем полностью, не разбивая ее на части.

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.