Во-вторых: а как вообще в общепринятой теории вероятностей обходятся со случаями, когда вероятность каждого события из рассматриваемой алгебры событий равна 0?
Никак, потому что аксиомы теории вероятностей этого не допускают. Какую полезную информацию Вы хотите извлечь и такого "вероятностного пространства", где вообще все вероятности равны нулю?
Попробую переформулировать: меня интересует, можно ли построить теорию вероятностей так, чтобы сохранить интуитивное представление о том, что всякая вероятность есть не просто число между 0 и 1, а доля некоторой части от некоторого целого, содержащего эту часть.
А она так и построена. "Целое" — это множество всех элементарных исходов

с мерой

, произвольное событие

— его часть, а

— "доля" события

в

. А потом появляется условная вероятность

(предполагается, естественно, что

), которая прямо по определению есть та самая доля, которую событие

составляет от

, и эта условная вероятность удовлетворяет всем аксиомам вероятности, так что ежели

— вероятностное пространство, то и

— вероятностное пространство. Впрочем, "безусловная" вероятность

на самом деле такая же условная, только условия эти не указываются явно в обозначении вероятности, а учитываются при построении вероятностного пространства.
Мне всегда казалось, что генератор случайных чисел должен быть способен равновероятно сгенерировать любое число из определённого множества. В предложенном мной случае это множество всех целых нечётных чисел, а не множество, состоящее из одного числа 1.
И с какой вероятностью этот генератор выдаёт число

? Или

? Или

? А каждое из остальных нечётных целых чисел? Они ведь должны быть все одинаковыми (Вы сами этого захотели), а сумма их (поскольку события "генератор выдал число

" и "генератор выдал число

" при

несовместны) должна быть равна

.
А в теории вероятностей есть понятие симметрии?
Нет. Видите ли, прежде чем мы сможем воспользоваться теорией вероятностей, мы должны определить вероятностное пространство, то есть, задать множество элементарных исходов,

-алгебру событий и функцию "вероятность". Теория вероятностей начинает работать только после того, как всё это уже появилось. А как мы определим

,

и

— это наше дело, лишь бы все нужные аксиомы выполнялись. В данном случае мы видим, что рассматриваемая область симметрична, и хотим, чтобы элементы этой области (точнее, одноэлементные события) имели одинаковые вероятности. Исходя из этих соображений мы и делаем вывод, что каждая из "половин" области имеет вероятность
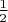
:
Конечно, можно генерировать только последние 6 цифр и знак числа. Тогда

- чисто из симметрии области

Здесь у нас область

содержит миллион нечётных не более чем шестизначных чисел от

до

, количество положительных и отрицательных чисел одинаковое, вероятности у них (исключительно по нашему желанию) одинаковые, вот и получается
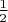
.
Вся классика ТВ построена на понятии симметрии.
Ну, здесь "симметрия" состоит исключительно в том, что вероятности всех элементарных исходов заранее предполагаются одинаковыми. Разумеется, число этих исходов должно быть конечным.