Да, я же привел пример выше. Там представляется в виде произведения только с комплексными коэффициентами и больше никак
Вообще-то, любой многочлен с действительными коэффициентами можно разложить в произведение многочленов с действительными коэффициентами степени не более

. Следует из того, что если

, где

, — комплексный корень многочлена с действительными коэффициентами некоторой кратности
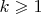
, то сопряжённое число

тоже является корнем этого многочлена, причём, той же кратности

.
Существует ли многочлен такого вида имеющий действительные корни, который нельзя представить в виде:

где

целые числа, которые могут быть равны нулю
Существует, конечно. Например:
