Ну вот, все готово, что бы разобраться. Итак, пусть

- центр исходного круга, тогда преобразование

переведет исходный круг в единичный. Если Ваше

то задача решена. Если нет, то все что остаётся в наличии - автоморфизм единичного круга

(
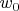
- образ точки

написанное переводит точку
в 0.) При этом, точки

и

куда-то уедут, и что бы вернуть их взад осталась единственная степень свободы - поворот круга как целого. Т.е. для произвольной

задача не решается, а для каких решается можно сообразить. Проблема в том, что у Вас было 3 с половиной условия (три точки и условие единичности радиуса), а параметров в дробно-линейном преобразовании только три, и эта половинка всю малину портит.