Думаю, что прошло достаточно времени, чтобы позволить чисто любительские соображения.
Все мы знаем, что синус от натурального аргумента всюду плотно заполняет интервал
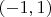
. Ясно, что возведение в фиксированную (ради сохранения интервала скажем, что нечётную) степень сносит значения к нулю, но всюдуплотность одолеть не сможет. Рассмотрим переменный (увеличивающийся) показатель степени. Очевидно, что снос к нулю будет всё сильнее. Весь вопрос в том, что будет происходить в окрестностях узловых точек, где синус близок по модулю к единице. Что победит: показатель степени или степень приближения? Если в последовательности есть бесконечно много членов, больших некоторого положительного числа, то ответом будет всюду плотное заполнение интервала. То есть любое число из интервала
![$[-1,1]$ $[-1,1]$](https://dxdy-03.korotkov.co.uk/f/6/9/9/699628c77c65481a123e3649944c0d5182.png)
будет предельной точкой. Мне кажется, что так оно и есть. Но тут надо, наверное, анализировать приближения

рациональными числами.
И ещё мне кажется, что показатель

не оставит надежды отличному от нуля числу

Я передумал!!!