гармонический осциллятор решение методом Эйлер (нужен совет)

[zxxrc19]

колебания простейшего гармонического осциллятора описываются следующем уравнением

$$\frac{d^2x}{dt^2}=-w^2x$$

Начальные условия: $ x=0$; $dx/dt=1 (t=0)$ .Решить данное уравнение при $w=6$ на интервале $0\leqslant t\leqslant3c$ усовершенствованным методом Эйлера.
Помогите пожалуйста хотя бы с методом решения. Как тут использовать усовершенствованный метод Эйлера для решения.
Проинтегрировал выражение :

$$\int (-\frac12w^2x^2+C)dx=-\frac16w^2x^2+Cx+C$$

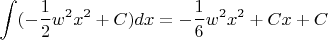
функция получилась такая :

$$f(y',y,x)=\frac12(y^2-2w^2xy)$$

попробовал подставить в формулу Эйлера {y}_{i+1}={y}_{i}+hf({x}_{i}+\frac{h}{2};{y}_{i}+\frac{h}{2}f({x}_{i};{y}_{i}))

надо все y заменить на столбцы $\binom{x}{x'}$

$$\left\{ \begin{array}{rcl} x'=x \\ (x')'=-{w}_{2}x \\ \end{array} \right.$$

[Slav-27]

А что такое усовершенствованный метод Эйлера? Это численный что ли?

Как можно решать аналитически: найти общее решение, а потом подобрать постоянные так, чтобы выполнялись начальные условия.

[photon]

Тема перемещена из форума «Помогите решить / разобраться (Ф)» в форум «Карантин»
по следующим причинам:

- неправильно набраны формулы (краткие инструкции: «Краткий FAQ по тегу [math]» и видеоролик Как записывать формулы);
- отсутствуют собственные содержательные попытки решения задач(и).

Исправьте все Ваши ошибки и сообщите об этом в теме Сообщение в карантине исправлено.
Настоятельно рекомендуется ознакомиться с темами Что такое карантин и что нужно делать, чтобы там оказаться и Правила научного форума.