Скаляр, псевдоскаляр, вектор и псевдовектор.

[Solaris86]

Здравствуйте. При знакомстве с темой умножения векторов (скалярное, псевдоскалярное, векторное, смешанное произведение, двойное векторное) я запутался в том, что является результатом каждого, и в обозначениях этих произведений. Прошу поправить там, где ошибки.
Я изучаю тему в связи с изучением физики (Савельев "Курс общей физики", том 1, параграф 2,). Серьёзной математической базы под всё это у меня нет, т.к. я только на втором курсе.
1. Скалярное произведение векторов $\mathbf{a}$ и $\mathbf{b}$:
1) обозначение: $\mathbf{a}\mathbf{b}, (\mathbf{a}\mathbf{b}), \mathbf{a} \cdot \mathbf{b}, (\mathbf{a} \cdot \mathbf{b}), (\mathbf{a},\mathbf{b}), <\mathbf{a},\mathbf{b}>, <\mathbf{a}|\mathbf{b}>$
2) выполнение: $\mathbf{a}\mathbf{b} = c = |\mathbf{a}||\mathbf{b}|\cos\alpha$
3) результат: скаляр c
2. Псевдоскалярное произведение векторов $\mathbf{a}$ и $\mathbf{b}$:
1) обозначение: $\mathbf{a}\vee\mathbf{b}$
2) выполнение: $\mathbf{a}\vee\mathbf{b} = c = |\mathbf{a}||\mathbf{b}|\sin\alpha$
3) результат: псевдоскаляр c
3. Векторное произведение векторов $\mathbf{a}$ и $\mathbf{b}$:
1) обозначение: $[\mathbf{a}\mathbf{b}], \mathbf{a}\times\mathbf{b}, [\mathbf{a}\times\mathbf{b}], [\mathbf{a},\mathbf{b}], \mathbf{a}\wedge\mathbf{b}$
2) выполнение: $[\mathbf{a}\mathbf{b}] = \mathbf{c}, c = |\mathbf{a}||\mathbf{b}|\sin\alpha$
3) результат: псевдовектор $\mathbf{c}$
4. Смешанное произведение векторов $\mathbf{a}$, $\mathbf{b}$ и $\mathbf{c}$:
1) обозначение: $\mathbf{a}[\mathbf{b}\mathbf{c}], (\mathbf{a}[\mathbf{b}\mathbf{c}]), \mathbf{a}\cdot[\mathbf{b}\times\mathbf{c}], (\mathbf{a}\cdot[\mathbf{b}\times\mathbf{c}]), (\mathbf{a},[\mathbf{b},\mathbf{c}]), (\mathbf{a},\mathbf{b},\mathbf{c})$
2) выполнение: $\mathbf{a}[\mathbf{b}\mathbf{c}] = |\mathbf{a}|(|\mathbf{b}||\mathbf{c}|\sin (\mathbf{b}, \mathbf{c}))\cos(\mathbf{a}, \mathbf{n})= d
3) результат: псевдоскаляр d
5. Двойное векторное произведение векторов $\mathbf{a}$, $\mathbf{b}$ и $\mathbf{c}$:
1) обозначение: $[\mathbf{a}[\mathbf{b}\mathbf{c}]], \mathbf{a}\times[\mathbf{b}\times\mathbf{c}], [\mathbf{a}\times[\mathbf{b}\times\mathbf{c}]], [\mathbf{a},[\mathbf{b},\mathbf{c}]], [\mathbf{a},\mathbf{b},\mathbf{c}]$
2) выполнение: $[\mathbf{a}[\mathbf{b}\mathbf{c}]] = \mathbf{b}(\mathbf{a}\mathbf{c}) - \mathbf{c}(\mathbf{a}\mathbf{b}) = \mathbf{d}, d = |\mathbf{b}(|\mathbf{a}||\mathbf{d}|\cos(\mathbf{a},\mathbf{c})) - \mathbf{c}(|\mathbf{a}||\mathbf{b}|\cos(\mathbf{a},\mathbf{b}))|
3) результат: вектор $\mathbf{d}$

Из этого всего я сделал вывод, что скаляр - это модуль вектора, а псевдоскаляр - это модуль псевдовектора.
Далее возник следующий вопрос: а что будет получаться в результате перемножения этих двух тензоров (скаляр - С и вектор В) и двух псевдотензоров (псевдоскаляр - ПС и псевдовектор - ПВ)?
Я попытался на него ответить и вот, что у меня получилось:
1. $\text{С}\cdot\text{С} = \text{С}$
2. $\text{С}\cdot\text{ПС} = \text{ПС}$
3. $\text{ПС}\cdot\text{С} = \text{ПС}$
4. $\text{ПС}\cdot\text{ПС} = \text{С}$
5. $\text{С}\cdot\text{В} = \text{В}$
6. $\text{С}\cdot\text{ПВ} = \text{ПВ}$
7. $\text{ПС}\cdot\text{В} = \text{ПВ}$
8. $\text{ПС}\cdot\text{ПВ} = \text{В}$
9. $\text{В}\cdot\text{В} = \text{С}$
10. $\text{В}\cdot\text{ПВ} = \text{ПС}$
11. $\text{ПВ}\cdot\text{В} = \text{ПС}$
12. $\text{ПВ}\cdot\text{ПВ} = \text{С}$
13. $\text{В}\vee\text{В} = \text{ПС}$
14. $\text{В}\vee\text{ПВ} = \text{С}$
15. $\text{ПВ}\vee\text{В} = \text{С}$
16. $\text{ПВ}\vee\text{ПВ} = \text{ПС}$
17. $\text{В}\times\text{В} = \text{ПВ}$
18. $\text{В}\times\text{ПВ} = \text{В}$
19. $\text{ПВ}\times\text{В} = \text{В}$
20. $\text{ПВ}\times\text{ПВ} = \text{ПВ}$

Что совершенно неясно:
1. Почему истинный вектор называется полярным, а псевдовектор - аксиальным (интересует именно смысл, который вложили в эти названия: при чём тут полюс для истинного вектора и ось для псевдовектора)?
2. Зачем зачем вообще отдельно вынесли псевдоскалярное произведение векторов, для чего оно нужно, ведь это всего навсего модуль псевдовектора из векторного произведения?
3. Что такое псевдоскаляр и зачем он вообще нужен? И чем он отличается от истинного скаляра.
4. Зачем нужна левая прямоугольная система, когда есть правая? Если правая основная, то почему в случае с двумя осями ось ОХ расположена по горизонтали, а OY - по вертикали? Я имею в виду то, что из левой системы OXYZ получить такую двухосевую OXY, где OX - горизонтальна, можно за один шаг - повернуть её на 90 градусов от нас вокруг оси OX, чтобы ось OZ исчезла, а а из правой системы её придётся получать за два шага: сначала повернуть на 90 градусов против часовой стрелки вокруг оси OZ, а затем на 90 градусов вокруг оси OX на нас. Где логика?
5. Все манипуляции с поворотами координатных осей. Я напрочь не понимаю, почему истинный и псевдовектор ведут себя по-разному.
Ну, вот для примера у нас правая прямоугольная система координат OXYZ и в ней несколько векторов:
- истинный вектор $\mathbf{c}$ с координатами $\mathbf{c} = \left\{0;0;6\right\}$
- псевдовектор $\mathbf{c'}$ с такими же координатами $\mathbf{c'} = \left\{0;0;6\right\}$, который получился в результате векторного умножения вектора $\mathbf{a}$ с координатами $\mathbf{a} = \left\{2;0;0\right\}$ на вектор $\mathbf{b}$ с координатами $\mathbf{b} = \left\{0;3;0\right\}$
Вот мы взяли и повернули эту систему вокруг оси OY на 180 градусов. Векторы $\mathbf{a}$ и $\mathbf{c}$ и псевдовектор $\mathbf{c'}$ повернулись также вокруг оси OX на 180 градусов, вектор $\mathbf{b}$ остался неподвижным. В итоге координаты всех векторов не изменились, поэтому координаты истинного вектора $\mathbf{c}$ и псевдовектора $\mathbf{c'}$ по-прежнему равны. И нет разницы между истинным вектором и псевдовектором. Или я что-то неверно понял, что такое инверсия системы координат? Ну даже если повернуть 3 раза вокруг всех трёх осей на 180 градусов, направления всех осей сменятся на противоположные, но координаты векторов-то останутся теми же самыми. Безусловно направления векторов относительно первоначального положения изменятся, но векторное произведение от этого не поменяется... В общем, с поворотами осей неясно.
Далее, при смещении начала системы координат будет всё аналогично в плане того, что все вектора передвинутся вместе с системой координат и этого межу ними относительно друг друга ничего не поменяет.
Единственное, что изменит положение дел - это перенос всех координат векторов из правой системы в левую. В левой системе векторное произведение вектора $\mathbf{a}$ с координатами $\mathbf{a} = \left\{2;0;0\right\}$ на вектор $\mathbf{b}$ с координатами $\mathbf{b} = \left\{0;3;0\right\}$ даст псевдовектор $\mathbf{c''}$ с координатами $\mathbf{c''} = \left\{0;0;-6\right\}$
Но тут опять становится непонятно: при переходе из правой системы в левую псевдовектор $\mathbf{c'} = \left\{0;0;6\right\}$ остался и стал истинным векторов в левой системе или вообще исчез и вместо него появился псевдовектор $\mathbf{c''} = \left\{0;0;-6\right\}$? Или сформулирую так по-другому: существует ли псевдовектор в отрыве от векторного произведения или он всё время вынужден следовать за парой породивших его векторов?
И еще такой неясный момент в связи с изменениями в системе координат: при изменениях в системе координат (повороты и/или сдвиги системы относительно центра и/или переход в "зеркальную" систему (левая <-> правая)) возможны следующие ситуации:
1. Вектор сохраняет направление относительно первоначального расположения осей и сохраняет значения координат неизменными (например, вектор $\mathbf{a}$ при поворотах вокруг оси OX).
2. Вектор меняет направление относительно первоначального расположения осей, но сохраняет значения координат неизменными (например, векторы $\mathbf{b}$ и $\mathbf{c}$, псевдовектор $\mathbf{c'}$ при поворотах вокруг оси OX).
3. Вектор сохраняет направление относительно первоначального расположения осей, но меняет значения координат (например, псевдовектор $\mathbf{c'}$ при повороте вокруг оси OX, а затем при переходе из правой системы в левую).
4. Вектор меняет направление относительно первоначального расположения осей и меняет значения координат (например, псевдовектор $\mathbf{c'}$ при переходе из правой системы координат в левую).
Получается, что 100% признак псевдовектора - это только изменение значений координат на противоположные, а изменение направления относительно первоначального расположения осей вовсе необязательно?
На этом примере, если не сложно, поясните и про истинный скаляр и псевдоскаляр, так как истинный скаляр (модуль вектора $\mathbf{c}$ равен 6) равен псевдоскаляру (модуль псевдовектора $\mathbf{c'}$ равен 6 и модуль псевдовектора $\mathbf{c''}$ тоже равен 6).

[Munin]

Много ерунды.

Давайте с начала.

Есть поле $K$ (это $\mathbb{R}$ или $\mathbb{C},$ его элементы дальше называются скалярами) и векторное пространство над ним $V(K).$ Это означает:
- что $K$ и $V$ образуют группы по сложению;
- и что $K\setminus\{0\}$ образует группу по умножению.

Update (17.11.2019): Я дурак. Забыл произведение скаляра на вектор. Это $K\times V\to V,$ со свойствами дистрибутивности по обоим аргументам.

Дальше вводятся операции векторного и скалярного произведений.

1. Скалярное произведение можно ввести всегда. Его тип: $V\times V\to K.$
2. А вот второе произведение можно ввести не всегда, в зависимости от размерности. Идея этого произведения - антикоммутативность.

В размерности 2, это будет "псевдоскалярное произведение" $\mathbf{a}\wedge\mathbf{b}=|\mathbf {a}|\cdot|\mathbf{b}|\sin\theta.$
В размерности 3, это будет векторное произведение $[\mathbf{ab}],\quad|[\mathbf{ab}]|=|\mathbf {a}|\cdot|\mathbf{b}|\sin\theta.$
А в других размерностях его ввести нельзя, точнее, существует его аналог - внешнее произведение - который только по случайному совпадению в размерностях 2 и 3 является скаляром или вектором.

Всё, больше никаких произведений нет.

( Точнее, есть ещё произведение 2 или 3 векторов, чтобы получить объём (скаляр).

В размерности 2 - это будет то же самое "псевдоскалярное произведение".
В размерности 3 - это будет выражение $(\mathbf{a}[\mathbf{bc}]).$
Оно выражается через другие произведения, и поэтому не является самостоятельной операцией. Впрочем, можно построить аксиомы и иначе, взяв это произведение за основу. )

Кроме этого, бывает приставка "псевдо", которая означает, что объект может менять или не менять знак при отражениях пространства, то есть, может иметь или не иметь множитель $(-1)^s.$

[arseniiv]

Munin в сообщении #1247296 писал(а):

который только по случайному совпадению в размерностях 2 и 3 является скаляром или вектором

Давайте уж точнее: в размерности 2 он является элементом одномерного векторного пространства $\Lambda^2 V$ над $K$, канонически, однако, не изоморфного $K$; изоморфизм принесёт, скажем, форма объёма на $V$; в размерности 3 это тоже не будет элемент $V$, а будет элемент изоморфного, но не канонически, ему $\Lambda^2 V$, хотя форма объёма опять поможет в присутствии скалярного произведения, чтобы из оставшегося после свёртки с формой ковектора сделать вектор.

[Dan B-Yallay]

Munin в сообщении #1247296 писал(а):

Есть поле $K$ (это $\mathbb{R}$ или $\mathbb{C},$ его элементы дальше называются скалярами) и векторное пространство над ним $V(K).$ Это означает:
- что $K$ и $V$ образуют группу по сложению;

Что за группу образуют эти два объекта, можно пояснить?

[arseniiv]

Каждый со своей собственной операцией $+$.

[Munin]

arseniiv в сообщении #1247301 писал(а):

Давайте уж точнее

Давайте нет. Обсуждать заточку мечей можно не в присутствии новичка, который пока простейших вещей не понимает.

Dan B-Yallay
К сожалению, у меня нет для вас ответа, вписывающегося в цензуру, принятую на этом форуме.

[arseniiv]

Munin в сообщении #1247315 писал(а):

Обсуждать заточку мечей можно не в присутствии новичка, который пока простейших вещей не понимает.

Так ведь они почти непосредственно связаны с тем, чем псевдо… отличаются от …, и почему их нельзя раз и на всегда взять и сложить в одну кучу. Хотя я соглашусь, что слова страшные: неканонический изоморфизм, форма объёма, свёртка.

[Dan B-Yallay]

arseniiv в сообщении #1247312 писал(а):

Каждый со своей собственной операцией $+$.

Тогда наверное правильней не "группу", а группЫ. И не образуют, а являются.
Тем не менее, спасибо за перевод на нормальный русский язык.

-- Вт сен 12, 2017 11:57:03 --

(Оффтоп)

Munin в сообщении #1247315 писал(а):

К сожалению, у меня нет для вас ответа, вписывающегося в цензуру, принятую на этом форуме.

Думаю, по моему вопросу у вас даже и нецензурного ответа не будет.

Munin в сообщении #1164599 писал(а):

Моей активности в (М) нет. Это не мой раздел, я туда не хожу.

[Brukvalub]

Munin в сообщении #1247296 писал(а):

Есть поле $K$ (это $\mathbb{R}$ или $\mathbb{C},$ его элементы дальше называются скалярами) и векторное пространство над ним $V(K).$ Это означает:
- что $K$ и $V$ образуют группы по сложению;
- и что $K\setminus\{0\}$ образует группу по умножению.

Это не объяснение, а "суперпопса". Понятие "поле" вовсе не исчерпывается "группами по сложению и умножению". Предлагаю ТС не считать, что с помощью таких "разъяснений" он может понять, что такое поле и векторное пространство, а обратиться к учебникам по алгебре, где все это корректно объяснено.

[kp9r4d]

Solaris86 в сообщении #1247254 писал(а):

Но тут опять становится непонятно: при переходе из правой системы в левую псевдовектор $\mathbf{c'} = \left\{0;0;6\right\}$ остался и стал истинным векторов в левой системе или вообще исчез и вместо него появился псевдовектор $\mathbf{c''} = \left\{0;0;-6\right\}$? Или сформулирую так по-другому: существует ли псевдовектор в отрыве от векторного произведения или он всё время вынужден следовать за парой породивших его векторов?

Нет, инвариантного описания нету. Некоторые говорят что есть, мол псевдовектор - это 2-вектор элемент $\wedge^2 V$ но всё-таки псевдовектор - это нечто, что получается если применить звезду ходжа к элементу $\wedge^2 V$, а в звезде ходжа есть некоторая проблема в том, что она меняет знак, если сменить ориентацию. Есть конечно выход в том, чтобы рассматривать "пространство с фиксированной ориентацией" как единый тип, и тогда звезда ходжа $\star : \Omega^k (V, \mathcal{O}) \to \Omega^{n-k} (V, -\mathcal{O})$ будет дедйствовать в пространство с противоположной ориентацией. И так как на втором пространстве $(V, -\mathcal{O})$ есть своя звезда ходжа $\star'$ которая, как можно проверить, удовлетворяет соотношению $\star' = -\operatorname{inv} \star \operatorname{inv}^{-1}$, где $\operatorname{inv}: (V, \mathcal{O}) \to (V, -\mathcal{O})$ это естественный оператор "смены ориентации". То мы как раз и получим, что $\star \operatorname{inv} v = - \operatorname{inv} \star' v$ (диаграмма, которая хотелось бы чтобы коммутировала не коммутирует), т.е. при зсмене ориентации аргумента, значение меняется на $-1$. Поэтому можно думать не "псевдовектор - это странная неопределенная штука, которая ведет себя непонятно как", а "звезда ходжа - это странная операция, которая не уважает ориентацию". Но так-то это не очень удобный контекст, например всякие группы вида $GL_n$ теперь сложнее рассматривать, да и вообще любой оператор меняющий ориентацию теперь не эндоморфизм.

Ну, в общем я это к чему, я бы на вашем месте особо не заморачивался и пытался привыкнуть к мысли "псевдовектор - это фигня, которая как вектор, но нужно дописывать минус всякий раз, как мы меняем ориентацию", вы ещё спиноров не видели, в конце концов :з

[Slav-27]

Когда я увидел эту тему и стал писать ответ, я решил сначала изложить некоторую теорию, которую традиционно многие не понимают. Чем дальше я писал, тем больше хотелось написать, и в конце концов получился длинноватый текст. Предлагаю, тем не менее, попробовать его прочитать.

(Длинный текст)

Что такое векторы, псевдовекторы и т. д.

1. Предисловие

1.1. Что это за текст

Судя по тому, как подробно вы выписывали все эти произведения, вас довольно сильно это интересует. Поэтому я написал довольно длинный текст, который, как мне кажется, содержит некоторую полезную информацию, касающуюся вашего вопроса, и в то же время интересен сам по себе.

В этом тексте понятие вектора и связанные с ним понятия описываются несколько необычным (для студентов младших курсов) образом: с точки зрения теории представлений. Вернее, этот подход совершенно стандартен много где, в том числе в физике (посмотрите, например, вот на этот пост), но в книжках для младшекурсников про него почему-то пишут плохо -- и именно из-за этого, как мне кажется, возникают непонимания вроде вашего.

Вторая причина, по которой я это пишу -- мне в своё время не хватало подобного текста; я думаю, что если бы я узнал про это чуть раньше, то жить мне было бы чуть проще.

Я, впрочем, совершенно не уверен, что этот текст кому-то будет полезен, поэтому если непонятно -- не читайте, или оставьте на потом.

1.2. Основное пространство

Мы будем рассматривать $3$-мерное евклидово прстранство $V$. Это $3$-мерное вещественное векторное пространство с заданным на нём скалярным произведением. (Я подразумеваю, что вы это знаете, у вас линал же был?)

Группа линейных преобразований $V$, сохраняющих длины векторов, называется ортогональной и обозначается $O(3)$. Её подгруппа, состоящая из преобразований, которые сохраняют ещё и ориентацию (то есть туда входят только вращения, но не отражения), обозначается $SO(3)$.

Если $V$ одномерное, то про него можно думать как про прямую с отмеченной на ней точкой (т. е. нулём), если двумерное -- как про плоскость с отмеченным нулём, и т. д. Поэтому векторы нашего основного пространства $V$ я буду отныне называть точками. А обозначать их буду полужирным шрифтом.

Под системой координат на $V$ я буду понимать ортонормированный базис; иногда я буду писать просто базис, подразумевая, что он ортонормированный.

Все числа у нас вещественные.

1.3. О двусмысленности слова "вектор"

Слово вектор используют как минимум в 2 разных смыслах.

Во-первых, вектором называют просто любой элемент любого векторного пространства.

Во-вторых, есть более тонкое понятие, которое тоже называют вектор. В этом смысле говорят, например, что "псевдовектор не является вектором", или "тензор 2-го ранга не является вектором".

Одна из наших целей -- дать точное определение этого вектора во втором смысле слова.

Я не знаю, как избежать путаницы со словом вектор. Там, где совершенно необходимо будет указать на второй смысл слова, я буду писать дурацкую фразу "вектор в тонком смысле".

1.4. Забегаем вперёд

Сейчас мы выпишем определение этого "вектора в тонком смысле", а также псевдовектора, скаляра и псевдоскаляра. Одна из главных целей этого текста -- объяснить, откуда такие определения берутся.

Определение. Вектор в точке $\mathbf q$ пространства $V$ задаётся так: каждой системе координат (т. е. каждому ортонормированному базису) $e$ пространства $V$ ставится в соответствие тройка вещественых чисел $v=\begin{pmatrix}v^1\\ v^2\\ v^3\\ \end{pmatrix}$, причём эти столбцы для разных систем координат связаны следующим образом: пусть $v$ -- столбец для $e$, $v'$ -- столбец для $e'$ и $T$ -- (ортогональная) матрица перехода от $e$ к $e'$; тогда $v=T v'$.

Определение псевдовектора точно такое же, за исключением того что закон преобразования $v=(\det T) \cdot Tv'$.

Определение скаляра: каждому базису $e$ ставится в соответствие число $s$, причём для всех базисов число одно и то же.

Определение псевдоскаляра: каждому базису $e$ ставится в соответствие число $s$, причём если базисы $e$ и $e'$ одинаковой ориентации, то число одно и то же, а если разной, то числа отличаются знаком: $s=-s'$.

Все эти штуки считаются прикреплёнными к какой-нибудь точке $\mathbf q$ пространства $V$, хотя в самом определении она не участвует.

Вся остальная часть текста представляет собой подробное пояснение этих четырёх определений. Больше там ничего принципиально нового по сути нет.

2. Обозначения

Здесь выписаны некоторые общепринятые соглашения; возможно, вы уже их знаете.

(Оффтоп)

2.1. Обозначения компонент векторов, операторов...

Пусть задан базис $e=(\mathbf e_1, \mathbf e_2, \mathbf e_3)$. Любой вектор по нему раскладывается: $v=v^1\mathbf e_1+v^2\mathbf e_2+v^3\mathbf e_3=\sum\limits_{i=1}^3v^i\mathbf e_i$. Это записывают ещё короче, пропуская знак суммы: $v=v^i\mathbf e_i$.

Вообще, если в произведении каких-то букв с индексами один и тот же индекс встречается дважды, причём один раз сверху, другой снизу, то подразумевается суммирование по всем значениям, которые он может принимать. Например, $T_{ij}v^iv^j$ означает $T_{11}v^1v^2+T_{12}v^1v^2+...+T_{33}v^3v^3$ (всего 9 слагаемых). Это соглашение называют соглашением Эйнштейна. Индексы в таком случае называются связанными; неважно, какой буквой их обозначать. Например $v^i x_i=v^j x_j=v^\aleph x_\aleph...$ Важно только, чтобы разные пары связанных индексов обозначались разными буквами.

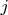
Пусть $v$ вектор, а $M$ линейный оператор. У него есть матрица $M_e$ в базисе $e$; её элемент в $i$-й строке и $j$-м столбце обозначают ${M^i}_j$. Пусть $u=Mv$; тогда в компонентах это запишется $u^i={M^i}_j v^j$.

2.2. Как обозначают компоненты, если используется 2 разных базиса

Часто приходится рассматривать 2 базиса $e$ и $e'$.

Тут примем такое соглашение: векторы базиса $e$ обозначаются $\mathbf e_1, \mathbf e_2, \mathbf e_3$ и вообще $\mathbf e_i$ (индекс $i$ пробегает значения $1, 2, 3$), а векторы базиса $e'$ обозначаются $\mathbf e_{1'}, \mathbf e_{2'}, \mathbf e_{3'}$ и вообще $\mathbf e_{i'}$ ($i$ опять пробегает значения $1, 2, 3$).

Вообще условимся обозначать то, что относится к базису $e$, индексами без штрихов, а то, что относится к $e'$ -- индексами со штрихами. В любой паре связанных индексов у нас будут либо оба со штрихами, либо оба без штрихов. Разложения вектора $v$ при таком соглашении записываются $v=v^i\mathbf e_i= v^{i'}\mathbf e_{i'}$.

Пусть $T$ -- линейное преобразование, переводящее базис $e$ в $e'$ (то есть вектор $\mathbf e_{i}$ в $\mathbf e_{i'}$). Компоненты матрицы $T_{e}$ записывают ${T^{i}}_{i'}$, так что $\mathbf e_{i'}=T(\mathbf e_i)=\mathbf e_{i}{T^{i}}_{i'}$.

Пусть вектор $v=v^i\mathbf e_i= v^{i'}\mathbf e_{i'}$; посмотрим, как выразить одни компоненты через другие, зная компоненты $T$. Выписываем: $v = v^{i'} \mathbf e_{i'} = v^{i'}\mathbf e_{i}{T^{i}}_{i'} = ({T^{i}}_{i'}v^{i'})\mathbf e_{i}$. То есть $v^i={T^{i}}_{i'}v^{i'}$.

Словами: столбец вектора $v$ в новом базисе = матрица перехода от нового базиса к старому (!) умножить на столбец в старом. -- Известное правило линейной алгебры.

Примечание. Используют ещё другую систему обозначений: пишут штрихи не у индексов, а у самого символа, так что разложение вектора по двум разным базисам записывается $v=v^i\mathbf e_i={v'}^i\,\mathbf {e'}_{i}$, и т. д.

Преимущество такого способа заключается в том, что для многоиндексных символов получается меньше штрихов. Недостаток же в том, что в этой нотации проще написать неправильное выражение, которое выглядит как правильное (то есть написать бессмысленную свёртку по индексам, относящимся к разным базисам).

2.3. Два вспомогательных символа

Символ Кронекера $\delta_{ij}$ -- это просто единичная матрица ($\delta_{11}=\delta_{22}=\delta_{33}=1$, остальные ноль).

Символ Ле́ви-Чиви́ты $\varepsilon_{ijk}$ меняет знак при обмене любых 2 индексов местами, причём $\varepsilon_{123}=1$. Он однозначно определяется этими условиями: $\varepsilon_{213}=\varepsilon_{132}=-1$; если хотя бы 2 индекса одинаковые, то он равен 0, и т. д.

Условимся, что индексы у этих символов можно писать хоть вверху, хоть внизу: ${\delta_i}^j$, $\varepsilon^{i j \phantom k}_{\phantom i\phantom j k}$ и т. д.

С помощью символа Леви-Чивиты удобно записывать векторное произведение: $a\times b = (a^1\mathbf e_1+a^2\mathbf e_2+a^3\mathbf e_3)\times (b^1\mathbf e_1+b^2\mathbf e_2+b^3\mathbf e_3) =$
$= a^1b^2 \mathbf e_1\times\mathbf e_2 + a^2b^1 \mathbf e_2\times\mathbf e_1+a^2 b^3 \mathbf e_2\times\mathbf e_3 + a^3b^2 \mathbf e_3\times\mathbf e_2+a^3b^1 \mathbf e_3\times\mathbf e_1+a^1b^3 \mathbf e_1\times\mathbf e_3=$
$=(a^2b^3-a^3b^2)\mathbf e_1 + (a^3b^1-a^1b^3) \mathbf e_2 + (a^1b^2-a^2b^1)\mathbf e_3$, так что $(a\times b)^i={\varepsilon^i}_{jk}a^jb^k$.

3. Наводящие соображения. Система координат как "точка зрения"

3.1. Объект, прицепленный к точке основного пространства

Предположим, мы хотим задать в некоторой точке $\mathbf q$ пространства $V$ какой-то объект. Каким образом можно это сделать?

Один из способов -- нельзя сказать что самый хороший, но часто довольно удобный -- ввести координаты на $V$ и описать объект с использованием координат. Неудобство этого способа состоит в том, что при изменении системы координат на $V$ описание объекта изменится.

3.2. Пример: скорость

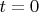
Предположим, что через точку $\mathbf q$ пространства $V$ в момент времени $t=0$ пролетает какая-то частица, и мы хотим прицепить к точке $\mathbf q$ скорость частицы в этой точке. (Скорость -- это, как известно, вектор. Причём слово вектор здесь надо понимать, как мы увидим, в тонком смысле.)

Пусть траектория частицы задаётся соответствием $t\mapsto \mathbf r(t)$, где $\mathbf r(t)$ -- какая-то известная функция одной переменной -- времени $t$ -- принимающая значения в $V$. Разумеется, $\mathbf r(0)=\mathbf q$.

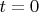
Введём координаты на $V$, тогда наша функция запишется в координатах $t\mapsto \begin{pmatrix} r^1(t)\\ r^2(t) \\ r^3(t) \end{pmatrix}$, причём при $t=0$ будет, конечно же, $r^i(0)=q^i$. Теперь определим $3$ числа $u^i$ следующим образом: $u^i={\frac {dr^i(t)} {dt}}\Big|_{t=0}$. Хочется думать, что эти числа определяют скорость частицы.

Но заковыка вот в чём. Сама частица никак не зависит от системы координат, то есть от той точки зрения, с которой мы на неё смотрим. Она вообще, может быть, не знает, что мы на неё смотрим и ввели какие-то координаты. Поэтому хочется думать, что и её скорость от координат не зависит.

Однако числа $u^i$ зависят от координат: если мы изменим координаты на $V$, то получим (вообще говоря) другой набор чисел -- проверьте! Получается, что, выбирая систему координат, мы смотрим на скорость с какого-то боку; если смотрим по-разному, то она и выглядит по-разному.

(Здесь я повторю, что описывать векторную величину, глядя на неё из какой-то системы координат -- не единственный возможный способ. Можно как-то обходиться и без координат. Но про это мы здесь говорить не будем.)

3.3. Вид объекта с разных "точек зрения"

Пусть мы хотим в точке $\mathbf q$ пространства $V$ задать некий объект $a$.

Мы будем выбирать системы координат и смотреть на объект из них. Видеть его из системы координат $e$ мы будем как элемент $a_e$ некоторого множества $D$. В случае скорости, $D$ -- это векторное пространство $\mathbb R^3$.

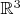
Мы хотим, чтобы описание нашего объекта $a$ в выбранной системе координат однозначно определяло объект. Это значит, что если задано описание $a_e$, то описание $a_{e'}$ должно быть какой-то определённой функцией от него: $a_{e'}=F_{e, e'}(a_e)$. (Вид функции $F_{e,e'}:D\to D$ зависит от того, какие базисы $e$ и $e'$ выбраны.)

Пусть теперь заданы два базиса $e$ и $e'$ и ещё два базиса $f$ и $f'$, причём линейное преобразование $T$ перехода от $e$ к $e'$ такое же, как от $f$ к $f'$. (То есть $T$ переводит $\mathbf e_i$ в $\mathbf e'_i$ и одновременно $\mathbf f_i$ в $\mathbf f'_i$.) Тогда (из соображений симметрии пространства $V$) разумно требовать, чтобы функция $F$ была одинаковой для той и для другой пары базисов. Поэтому будем считать, что $F$ зависит не от конкретного вида базисов $e$ и $f$, а только от соединяющего их ортогонального преобразования $T$; и будем обозначать $F_{e,e'}=F_{f,f'}=F_T$.

Если $T$ -- тождественное преобразование, то и $F_T$ должна быть тождественной функцией: не меняем точку зрения -- не меняется и то, что мы видим. Если $T$ и $U$ -- два ортогональных преобразования, то должно быть $F_{TU}=F_T\circ F_U$ (композиция функций): не имеет значения, изменили ли мы одну точку зрения на другую сразу, или же между ними прошли через какую-то третью.

В таких случаях говорят, что группа ортогональных преобразований действует на множестве $D$.
4. Представления

Итак, группа $G$ действует на множестве $D$ -- это значит вот что: каждому элементу группы поставлено в соответствие преобразование (биекция) $D\to D$, причём единице группы соответствует тождественное преобразование, а произведению элементов группы -- композиция преобразований.

Если $D$ -- векторное пространство, то говорят также, что задано представление этой группы преобразованиями пространства $D$. Если эти преобразования линейные, то говорят линейное представление. Нередко говорят просто представление, подразумевая, что оно линейное.

Сказанное выше сводится к следующему алгебраическому определению: (линейное) представление группы $G$ в $d$-мерном векторном пространстве -- это гомоморфизм $G\to GL(d)$.

Преобразование $F_T$, соответствующее элементу $T$, называют представителем элемента $T$.

Наука, которая изучает представления групп, называется теория представлений.

Представления $G\to GL(d)$ называются эквивалентными, если они отличаются на замену базиса в этом $d$-мерном пространстве.

4.1. Продолжение примера про скорость

Посмотрим, по какому представлению ортогональной группы преобразуется столбец $u^i$, которым мы хотим описывать скорость.

Но сначала подумаем: а какие вообще могут быть $3$-мерные линейные представления $O(3)$?

Глупый пример -- тривиальное 3-мерное представление: все элементы группы представляются тождественным преобразованием. То есть столбец вообще не меняется. Как скоро увидим, построенный нами столбец ведёт себя не так.

Ещё один очевидный пример. По самому определению элементы группы $O(3)$ -- это какие-то линейные преобразования 3-мерного векторного пространства; значит, просто по определению имеет место некоторое линейное 3-мерное представление этой группы. Это представление называется векторным. Если задан базис $e$, то действие элемента $R$ на вектор $\mathbf v$ (по векторному представлению) записывается $v^i \mapsto {R^i}_{j}v^j$; это просто умножение матрицы на столбец. Сейчас мы увидим, что столбец скорости преобразуется именно по этому представлению:

У нас была функция $t\mapsto \mathbf r(t)$. В базисе $e'$ это выглядит $t\mapsto r^{i'}(t)$, и компоненты скорости, по нашему определению, $u^{i'}=\frac{dr^{i'}(t)}{dt}\Big|_{t=0}$. Пусть есть другой базис $e$, тогда $r^i={T^i}_{i'}r^{i'}(t)$, и по нашему определению $u^i=\frac{dr^{i}(t)}{dt}\Big|_{t=0}= {T^i}_{i'} \frac{dr^{i'}(t)}{dt}\Big|_{t=0}={T^i}_{i'}u^{i'}$.

Итак, скорость, торчащая из точки $\mathbf q$ пространства $V$, преобразуется при ортогональных преобразованиях пространства $V$ по тому же представлению ортогональной группы, по которому преобразуются сами "точки" простанства $V$. С одной стороны, это очевидно. С другой стороны, это нетривиальный факт, потому что подчёркиваю ещё раз: скорость, торчащая из $\mathbf q$ -- это не элемент $V$!

4.2. Сумма представлений

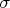
Пусть $m$-компонентный столбец $u^i$ преобразуется по представлению $\rho$, а $n$-компонентный столбец $v^i$ -- по представлению $\sigma$; можно составить из них один $(m+n)$-компонентный столбец $w^i$ с компонентами $(u^1, ..., u^{m}, v^1, ..., v^{n})$; представление, по которому он преобразуется, называется прямой суммой $\rho\oplus\sigma$.

Тут как будто нет ничего интересного: задать объект $w^i$ -- это всё равно, что задать пару объектов $u^i$ и $v^i$.

Если представление нельзя разложить в (нетривиальную) прямую сумму, то оно называется неразложимым. (Если у представления нет нетривиальных подпредставлений, то оно называется неприводимым. В случае ортогональной группы неразложимость и неприводимость -- одно и то же, поэтому не будем в это вдваваться.)

4.3. Произведение представлений

Можно также из $u^i$ и $v^i$ составить $mn$-компонентный объект $T^{ij}=u^i v^j$ (тензорное произведение $u^i$ и $v^i$). Представление, по которому он преобразуется, называется тензорным произведением представлений $\rho\otimes\sigma$.

Например, если $u^i$ и $v^j$ -- векторы (как вектор скорости из нашего примера), то их произведение $T^{ij}$ преобразуется по закону $T^{ij}=u^iv^j = {R^i}_{i'} u^{i'} {R^j}_{j'}v^{j'} ={R^i}_{i'} {R^j}_{j'}T^{i'j'}$.

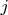
Так же определяется тензорное произведение более чем 2 объектов, в результате получаются объекты с 3 индексами, с 4 и т. д. Разумеется, количество индексов не имеет особенного значения: в конце концов можно вместо 2 индексов $i$ и $j$ ввести один индекс, изменяющийся от $1$ до $mn$. Но если объект преобразуется по тензорному произведению каких-то представлений, то гораздо удобнее оставить несколько индексов.

5. Представления $SO(3)$

Какие вообще бывают представления $SO(3)$? Теория представлений даёт ответ на этот вопрос:

Теорема. В каждой нечётной размерности у $SO(3)$ есть ровно одно (с точностью до эквивалентности) неприводимое представление. В чётных размерностях неприводимых представлений нет.

Неприводимое представление $SO(3)$ можно обозначать числом, соответствующим размерности: $\mathbf 1, \mathbf 3, \mathbf 5$ и так далее.

Первые 2 мы уже знаем: $\mathbf 1$ -- это тривиальное или скалярное представление, а $\mathbf 3$ -- векторное.

Остальные неприводимые представления сами по себе нам не интересны пока. (А вот когда будете изучать квантовую механику, всякие там повороты и прочий атом водорода -- тогда узнаете и про них, и про сферические гармоники...)

Но интересны произведения векторных представлений $\mathbf 3\otimes \mathbf 3$, $\mathbf 3\otimes\mathbf 3\otimes\mathbf 3$ и т. д., по которым преобразуются тензоры. (Они приводимы, но это нам тоже пока не надо знать.)

(Оффтоп)

5.1. Добавление: разложение представления $\mathbf 3\otimes \mathbf 3$ на неприводимые

Представление $\mathbf 3\otimes \mathbf 3$ имеет, очевидно, размерность $9$. Но оно приводимо, как мы сейчас увидим, так что это не $\mathbf 9$.

Пусть $T^{ij}$ -- тензор, преобразующийся по представлению $\mathbf 3 \otimes \mathbf 3$. Любую матрицу $T^{ij}$ можно разложить на симметричную и антисимметричную часть: $T^{ij}=\frac 12 (T^{ij}+T^{ji}) + \frac12 (T^{ij}-T^{ji})=S^{ij}+A^{ij}$. (То есть $S^{ij}=S^{ji}$, а $A^{ij}=-A^{ji}$.) Симметричную часть можно ещё разложить на скалярную и бесследовую: $S^{ij}=\frac13\operatorname{tr}S\, \delta^{ij}+ \tilde {S}^{ij}$ (след матрицы есть $\operatorname{tr}S={S^i}_i$ -- сумма диагональных элементов).

Несложно проверить, что "скалярный" тензор преобразуется при вращении в "скалярный", симметричный бесследовый в симметричный бесследовый, а антисимметричный -- в антисимметричный. Значит, мы разбили наше представление на 3 прямых слагаемых.

1. Скалярная часть. У скалярной матрицы только 1 независимый элемент, поэтому соответствующее прямое слагаемое есть $\mathbf 1$. Очевидно, что эта часть действительно преобразуется тривиально (след не меняется при изменении базиса).

2. Антисимметричная часть. У антисимметричной матрицы $A^{ij}=\begin{pmatrix}0 & a & b\\ -a & 0 & c\\ -b & -c & 0\end{pmatrix}$ всего $3$ независимые компоненты (те, что над главной диагональю). Значит, соответствующее представление либо $\mathbf 1 \oplus \mathbf 1 \oplus \mathbf 1$, либо $\mathbf 3$. Но оно явно нетривиально, поэтому $\mathbf 3$ (с точностью до эквивалентности!).

Раз представление эквивалентно $\mathbf 3$, то, по определению, его можно превратить в $\mathbf 3$ выбором базиса в 3-мерном векторном пространстве антисимметричных матриц. Скажем это же по-другому: можно установить линейное взаимно-однозначное соответствие между антисимметричными $3\times 3$ матрицами и $3$-компонентными столбцами таким образом, что соответствующий матрице $A^{ij}$ столбец $B^i$ будет преобразовываться в точности как вектор. Проверьте, что такое соответствие устанавливается формулой $B^i=\frac 12 {\varepsilon^i}_{jk}A^{jk}=\begin{pmatrix}c\\ -b\\ a\\ \end{pmatrix}$.

3. Симметричная бесследовая часть. У симметричной матрицы 6 независимых компонент, поэтому у симметричной бесследовой 5. Можно доказать, что соответствующее представление неприводимо (но мы не будем).

Итак, $\mathbf 3 \otimes \mathbf 3= \mathbf 5 \oplus \mathbf 3 \oplus \mathbf 1$.

6. Представления $O(3)$

Мы пока говорили о представлениях $SO(3)$; эта группа включает только повороты, но не отражения. А какие бывают неприводимые представления $O(3)$?

Так как $SO(3)\subset O(3)$, то каждое представление $O(3)$ -- это расширение какого-то представления $SO(3)$.

Обозначим отражение относительно всех координатных осей буквой $P$ (оно переводит $v$ в $-v$). Любое несобственное ортогональное преобразование (в нечётной размерности!) представляется в виде композиции $P$ и какого-то собственного преобразования. Поэтому достаточно знать представление $SO(3)$ да ещё представитель оператора $P$ -- и будет определено всё представление $O(3)$.

Заметим, что $P^2=1$ -- тождественное преобразование.

6.1. Размерность 1: скаляры и псевдоскаляры

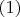
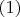
У $SO(3)$, как мы знаем, есть единственное 1-мерное представление $\mathbf 1$ -- тривиальное: каждое вращение представляется $1\times 1$ матрицей $(1)$. Так как $P^2=1$, то его представителем может быть только $(1)$ или $(-1)$.

Первый выбор даёт тривиальное представление $O(3)$ -- обозначим его $\mathbf {+1}$; оно называется ещё скалярным, а соответствующие объекты -- скаляры. Они вообще не меняются.

Второй выбор даёт представление, которое мы обозначим $\mathbf {-1}$; оно называется псевдоскалярным, а соответствующие объекты -- псевдоскаляры. Псевдоскаляры не меняются при повороте, а при отражении меняют знак.

Упражнение: проверьте, что смешанное произведение векторов $a\cdot(b\times c)=\varepsilon_{ijk}a^ib^jc^k$ -- псевдоскаляр.



(Внимание! Обозначения представлений $O(3)$ с плюсами и минусами, которые я сейчас начинаю использовать -- не общеупотребительны.

Ещё мы будем иногда пропускать плюсы, то есть писать $\mathbf 1$ вместо $\mathbf {+1}$.)

6.2. Размерность 3: векторы и псевдовекторы

Там всё аналогично: можно убедиться, что $P$ можно представлять только либо минус единичной, либо плюс единичной матрицей.

Соответственно получаем представление $\mathbf {+3}$ (соответствующие объекты называются векторы -- вот они, векторы в тонком смысле!) и $\mathbf {-3}$ (соответствующие объекты -- псевдовекторы).

На всякий случай выпишем тут полностью законы преобразования. Векторы преобразуются по закону $u^i={R^i}_{j'}u^{j'}$. Псевдовекторы при поворотах преобразуются по такому же закону, а при несобственных преобразованиях -- по закону $u^i=-{R^i}_{j'}u^{j'}$; это можно объединить в одну формулу для псевдовекторов: $u^i=(\det R)\; {R^i}_{j'} u^{j'}$.

Упражнение: проверьте, что векторное произведение векторов $(a\times b)^i={\varepsilon^i}_{jk}a^jb^k$ -- псевдовектор.

6.3. Неприводимые представления размерности выше 3

Они нас не интересуют. Впрочем, там всё так же:

Теорема. Каждому неприводимому представлению $\mathbf d$ группы $SO(3)$ ($d$ нечётное, конечно же) соответствуют ровно 2 представления $O(3)$ (обозначаем их $\mathbf {+d}$ и $\mathbf {-d}$). Других конечномерных неприводимых представлений нет.

6.4. Тензоры и псевдотензоры

Рассмотрим произведения векторных и псевдовекторных представлений. Непосредственно из формул преобразования очевидно, что $\mathbf {3} \otimes \mathbf {-3} = \mathbf {-3} \otimes \mathbf {3}$, а $\mathbf {-3} \otimes \mathbf {-3} = \mathbf {3} \otimes \mathbf {3}$ и т. д., поэтому тензорные произведения можно обозначать просто $\mathbf {3} \otimes \mathbf {3}$, $ - \mathbf {3} \otimes \mathbf {3}$ и т. д., вынося знак вперёд.

Если получился знак плюс, то объекты, преобразующиеся по этому представлению, называются тензоры (2-го, 3-го... ранга соответственно количеству троек в произведении), а если минус -- псевдотензоры (соответствующего ранга).

(Псевдо)векторы можно рассматривать как (псевдо)тензоры 1-го ранга, а (псевдо)скаляры -- нулевого.

7. Что бывает, когда размерность основного пространства не 3

Мы везде считали, что основное пространство $V$ 3-мерно, и поэтому изучали представления группы $O(3)$.

В случае $n$-мерного пространства нам пришлось бы изучать представления группы $O(n)$. Они, вообще говоря, устроены по-другому.

Но тензоры можно использовать в любой размерности: понятно, что есть аналогичные $1$-мерное тривиальное или скалярное представление, $n$-мерное векторное, и тензорные представления -- тензорные степени фундаментального.

Точно так же в любой размерности можно определять псевдоскаляры, псевдовекторы, псевдотензоры -- добавляя в соответствующую формулу преобразования множитель $\det T=\pm 1$.

Теперь пробую ответить на ваши вопросы.

Solaris86 в сообщении #1247254 писал(а):

скаляр - это модуль вектора, а псевдоскаляр - это модуль псевдовектора.

Первое верно, второе нет. Скалярный квадрат псевдовектора -- истинный скаляр ($(\det R)^2=1$ для любой ортогональной матрицы), модуль -- это положительный квадратный корень из него, так что тоже истинный скаляр...

Solaris86 в сообщении #1247254 писал(а):

при чём тут полюс для истинного вектора и ось для псевдовектора

Угловая скорость -- это псевдовектор, направленный вдоль оси вращения; вероятно отсюда. Насчёт полюса не знаю.

Solaris86 в сообщении #1247254 писал(а):

Зачем зачем вообще отдельно вынесли псевдоскалярное произведение векторов, для чего оно нужно

Лично я ни разу до этой темы его не видел, так что подозреваю, что оно мало зачем нужно. Тем не менее конструкция естественная. Но она определена только в плоскости! В 3-мерном пространстве непонятно, в какую сторону мерить угол (даже если сказано, какая 3-мерная система координат правая).

Solaris86 в сообщении #1247254 писал(а):

Зачем нужна левая прямоугольная система, когда есть правая? Если правая основная, то почему в случае с двумя осями ось ОХ расположена по горизонтали, а OY - по вертикали? Я имею в виду то, что из левой системы OXYZ получить такую двухосевую OXY, где OX - горизонтальна, можно за один шаг - повернуть её на 90 градусов от нас вокруг оси OX, чтобы ось OZ исчезла, а а из правой системы её придётся получать за два шага: сначала повернуть на 90 градусов против часовой стрелки вокруг оси OZ, а затем на 90 градусов вокруг оси OX на нас. Где логика?

Тут надо разделять 2 вещи: 1) какой базис считают правым, 2) как рисуют картинки.

Если задана основная система координат, то на плоскости считают правым базис $(\mathbf e_x, \mathbf e_y)$, в 3-мерном пространстве -- $(\mathbf e_x, \mathbf e_y, \mathbf e_z)$ и т. д. -- вне зависимости от того, как это нарисовано на картинке.

Рисуют же 3-мерную систему координат обычно таким образом, чтобы точки, у которых все координаты положительны, не были закрыты от зрителя другими октантами.

Solaris86 в сообщении #1247254 писал(а):

Все манипуляции с поворотами координатных осей. Я напрочь не понимаю, почему истинный и псевдовектор ведут себя по-разному.

Отражение поворотами не получается! Вы можете повернуть левую перчатку так, чтобы она совпала с правой? Я нет. Так что вот это вот

Solaris86 в сообщении #1247254 писал(а):

даже если повернуть 3 раза вокруг всех трёх осей на 180 градусов, направления всех осей сменятся на противоположные

-- неверно.

[Dan B-Yallay]

Slav-27
Замечательное изложение под "длинным текстом". Предлагаю модераторам перенести копию в матсправочник.

[Munin]

Slav-27 в сообщении #1248736 писал(а):

Во-вторых, есть более тонкое понятие, которое тоже называют вектор. В этом смысле говорят, например, что "псевдовектор не является вектором", или "тензор 2-го ранга не является вектором".

Одна из наших целей -- дать точное определение этого вектора во втором смысле слова.

Я не знаю, как избежать путаницы со словом вектор. Там, где совершенно необходимо будет указать на второй смысл слова, я буду писать дурацкую фразу "вектор в тонком смысле".

Afaik, этот смысл выражается оборотом "вектор данного пространства", который часто сокращается до просто "вектор".

[kp9r4d]

Подход с представлениями тоже видел, но он плохо вяжется с формализмом геометрического калькулюса - веджами, диезами, бемолями и звёздами всякими, - что печалит немного.

[Slav-27]

kp9r4d
Зато хорошо вяжется со спинорами. Они получаются совершенно так же, надо только вместо линейных представлений брать проективные (причём известно, что они в некотором хорошем смысле сводятся к линейным, для них в нужных случаях есть классификация и т. д.). Я думаю, это одна из причин, по которой во многих книжках по физике используют что-то похожее именно на этот подход. Да и вообще представления много для чего полезны, симметрии тензора кривизны изучать, например.

То есть я не говорю, что надо срочно всех переучивать, наоборот, но в курсе вот про это быть, по-моему, полезно.

(Геометрический калькулюс)

Осторожно, в последнее время словом geometric calculus называется какая-то штука на основе алгебр Клиффорда. Что у них там концептуально нового и есть ли от этого какая-то польза, я пока не понял. (У меня вообще сложилось впечатление, что это сейчас активно толкают какие-то примерно пять человек, а остальным пофигу.) Ещё я читал, что они переформулировали с использованием этой штуки ОТО и получили что-то очень похожее, но не вполне эквивалентное. Возможно, это чушь, не знаю, если кто в курсе, скажите.